Numbers

tags : Math

95% of the numbers that you use were invented to solve equations. Probably the least important property of these things, mathematically at least, is their decimal expansion. Their corresponding equations are infinitely more vital.

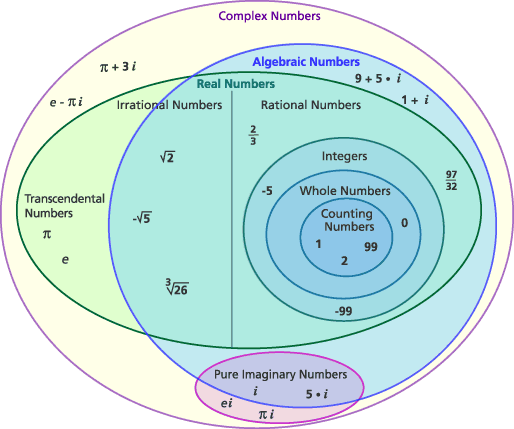
I believe the fundamental problem (or confusion) here is that OP finds it difficult to believe that a rational number, which is a ratio of two finite integers, can have a representation which is infinite. This confusion is primarily due to the fact that most people try to think of a number and its representation as one and the same thing. However the concept of a number is different from the concept of representing it.

Primitives §

Axioms §

• Minimum necessary subset of rules
• Greek axioma, ‘that which is self evident”

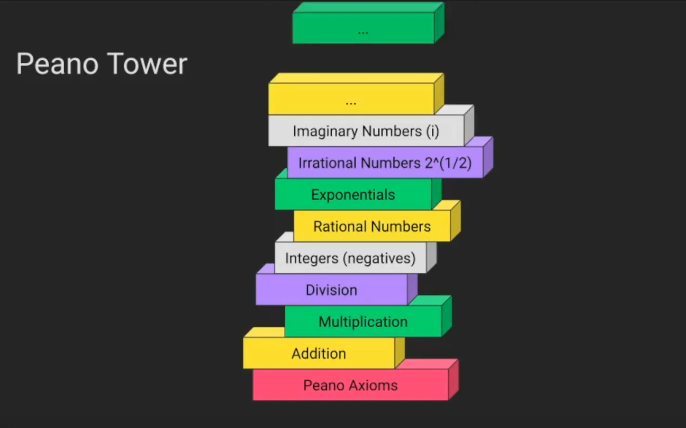
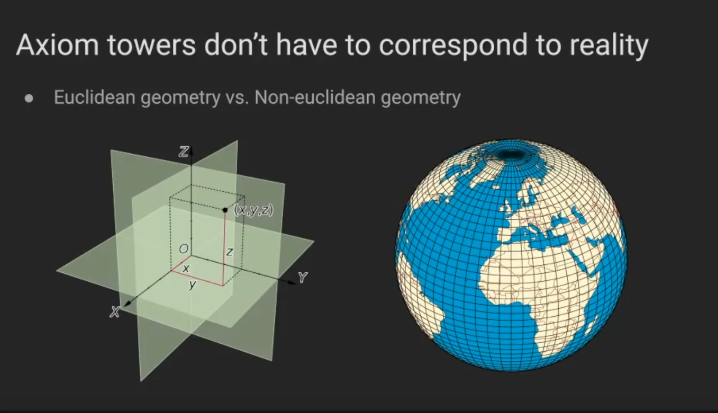
Theorems §

• We can call the derived rules theorems
• Greek theorema, “a proposition to be proved”

Symbols §

• Symbols used in math are contextual
• Eg. 0x20 means 32 in Hex, but space in ASCII
• So Symbols without the rules/context mean almost nothing.

Peano §

Peano’s Axioms §

• 1st Axioms were given by Peano. (S is Successor Function)

Addition and multiplication theorems §

• Devlin’s Angle: How multiplication is really defined in Peano arithmetic

FAQ §

• Is 0 a natural number? Sometimes, yes.
• What Does It Mean to Be a Number? (The Peano Axioms)
• How to Easily Memorize the Multiplication Table
• Ackermann function - Wikipedia