🐏 mogoz

Search

SearchSearch

Floating Point

Jun 30, 2024, 6 min read

tags : Math, Fixed Point

The term floating point refers to the fact that the number’s radix point can “float” anywhere to the left, right, or between the significant digits of the number. This position is indicated by the exponent, so floating-point can be considered a form of scientific notation.

Introduction

FP are just scientific notion

Advantage

  • Speed: Commonly measured in terms of FLOPS. (Okay THIS MIGHT BE WRONG) 
    # int
Integer add: 1 cycle
32-bit integer multiply: 10 cycles
64-bit integer multiply: 20 cycles
32-bit integer divide: 69 cycles
64-bit integer divide: 133 cycles
# float
Floating point add: 4 cycles
Floating point multiply: 7 cycles
Double precision multiply: 8 cycles
Floating point divide: 23 cycles
Double precision divide: 36 cycles
 
source: http://www.phys.ufl.edu/~coldwell/MultiplePrecision/fpvsintmult.htm
  • Efficiency : Can deal with really big and small numbers without needing large amount of space.

How

Without FPU

A floating-point unit(FPU) is a part of the processor specifically designed to carry out floating-point numbers ops.

With FPU

Bases

  • In practice, most floating-point numbers use base 2, though base10 (decimal floating point) is also common, there are also other bases used for FP.
  • The base determines the fractions that can be represented
    • 1/5 cannot be represented exactly as a floating-point number using a binary base
    • 1/5 can be represented exactly using a decimal base (0.2, or 2×10-1)
    • 1/3 cannot be represented exactly using binary or decimal base
    • 1/3 can be represented exactly using base 3 (0.1, or 1×3-1)

Anatomy

A floating-point format is specified by

  • Base (radix): b
  • Precision: p (significand, i think)
  • Exponent range: emin to emax, w emin = 1 − emax for all IEEE 754

Significand

A signed (+/-) digit string of a given length in a given base(radix).

  • This digit string is referred to as the significand, mantissa, or coefficient.
  • The radix(base) point position is always somewhere within the significand
  • The length of the significand determines the precision to which numbers can be represented.
  • Eg. p=24, b=2, single-precision(32bit) : significand will be string of 24 bits. So precision will be till 24bits.

Exponent

  • A signed integer exponent (also referred to as the characteristic, or scale)
  • Modifies the magnitude of the number.
    • eg. -5 is smaller than 3 but greater in magnitude than 3 (-5+3=-2)
  • The exponent shifts the radix point in the significand and changes the magnitude

Rounding and Error

Associativity and Commutativity

It’s not associative, not commutative

octave:1> x=0.1+0.2+0.3
x = 0.60000
octave:2> y=0.3+0.2+0.1
y = 0.60000
octave:3> x==y
ans = 0
octave:4> x-y
ans = 1.1102e-16

Deterministic?

  • They’re deterministic but partially implementation defined.
  • Some instructions don’t guarantee the maximum possible precision, and implementations can differ in the least significant bits of their result.
  • There are minor differences between hardware (x87 vs SSE is the most famous one, but there are others). Changing compiler, its version or options may produce subtly different results (the most obvious example is the -ffast-math flag). And even the bigger problem is implementation of non-primitive (e.g. trigonometric) functions. Usually your program will use implementation from a system or vendor library, which probably have different underlying implementations.

Precision (based on IEEE 754)

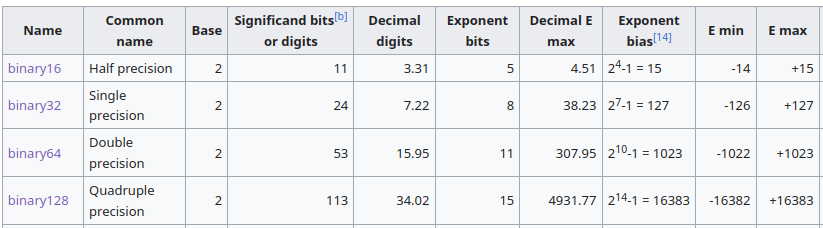
16-bit: Half (binary16)

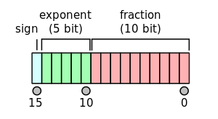
32-bit: Single (binary32)

64-bit: Double (binary64)

  • Can represent about 15 decimal digits of precision, enough to describe any position in the solar system with millimeter precision.

Extended precision

  • The x86 extended precision format is an 80-bit format
  • long double in C is 80bits

128-bit: Quadruple (binary128)

  • This has no hardware support
  • __float128 lacks hardware support, hence is slower than double.
  • Many space trajectory calculations use quadruple precision arithmetic, and most galactic evolution research considers statistical distributions rather than say something precise about the future state of the galaxy.

Arbitrary precision

  • Arbitrary-precision arithmetic
  • Implementations of much larger numeric types (w a storage count that usually is not a power of two) using special software
  • The dc and bc programs are arbitrary precision calculators
  • Javascript uses arbitrary precision for BigInt
  • IEEE754 does not require correctly rounded mathematical functions, it only recommends them. So, the accuracies vary from one mathematical library to another

When deciding what to use

For the same cost of doing a single float64 multiplication, you can do four float32 multiplications. So in practice, people choose the smallest data size that is good enough to work.

Floating Point and Processors

No FPU

What happens when certain precision is not supported by the CPU?

  • The quad precision software floating point should speed up slightly, but it’s still implemented in scalar integer arithmetic.

x87 co-processor

Languages usage

Javascript

See Javascript JS has just 2 number types

number

Uses double-precision 64-bit binary format IEEE 754 or binary64.

  • Safely represents between -(253 − 1) and 253 − 1 without loss of precision.
  • Number.MAX_VALUE : Largest number possible to represent
  • Number.MAX_SAFE_INTEGER : Largest integer to be used safely in calculations.
  • Number.MIN_SAFE_INTEGER : Smallest integer to be used safely in calculations.

BigInt

  • Numeric primitive in JavaScript that can represent integers with arbitrary precision.
  • Makes it possible to correctly perform integer arithmetic without overflowing.

Other notes

  • One of the other things in I-triple-E 754 floating point numbers is an explicit encoding for things that are not numbers, like infinity.

Resources

Basics

Wikipedia

Videos

Intermediate

Precision

Error

Graph View

Backlinks