Understanding Scales

tags : Economics , Math, Logarithm

I always get confused by scales, so i note them here for future ref of scales i come across often.

• This video nicely shows how rich Jeff Bezos is doe.
• $10^{13}$mts from wherever you’re reading this from, you could see the entire solarsystem infront of your eyes
• Orders of magnitude (numbers)
• Admiral Grace Hopper Explains the Nanosecond - YouTube

Decimal Separator §

One thing that ate my head initially was that some people use . as decimal separator. why bro?

million, billion, lakh, cr §

• 1bn = 100cr = 9 zeros = $10^9$
• 1cr = 10mn = 100lac = 7 zeros = $10^7$
• 1mn = 10lac = 6 zeros = $10^6$
• 1lac = $10^5$

For currency it’s again multiplying by the currency. Eg. To me a millionaire you’ll need:

$75.69\times 10^6\approx 7\text{*}10^7$, so if you have around ₹ 7cr in your bank, you’re a millionaire. 🤑

---

bandwidth, latency and throughput §

Layman explanation don’t ?? (????) me; You live in Guwahati and wish to send 200TiB of pirated ebooks to your friend in Delhi, out of may options here are two:

• Send it via mailpost (High Bandwidth, High Latency)
• Send it via IP Network/Internet (Low Bandwidth, Low Latency)

It’ll take a lot of time for your friend to download 200TiB of data with the Internet but will be able to stream it the fastest due to lower latency than sending it via mailpost.

• Bandwidth: Amount of data you can send. High Bandwidth is good.
• Latency: How much time it takes for a signal(in our case the first signal) to travel to its destination. Low Latency is good.
• Throughput: How much data is travelling. High Throughput is good.

---

Bytes §

• 1e+9 bytes = 1e9 = $10^9$B = 2^30B = 1GB (1 Billion bytes in 1GB)
• 1e+6 bytes = 1e6 = $10^6$B = 2^20B = 1MB (1 Million bytes in 1MB)
• 8bits = 1byte $⟹$ 500KB = 4000Kb = 4Mb
• 12Mbps connection = 1.5MBps (network uses bps)

The reason you choose one scale over another when graphing is to reveal detail that might otherwise be hidden by the nature of the data you’re looking at.

Signed & Unsigned integers §

There are arch dependent integer types such as int, uint these pick the length based on arch. Eg. on 64bit systems, int will be int64, uint will be uint64

Signed integers §

• int8: -1<<23-1 to 1<<(23-1)-1 : -128 to 127
• int16: -1<<24-1 to 1<<(24-1)-1 : -32768 to 32767
• int32: -1<<25-1 to 1<<(25-1)-1 : -2147483648 to 2147483647
• int64: -1<<26-1 to 1<<(26-1)-1 : -9223372036854775808 to 9223372036854775807

Unsigned integers §

• uint8: 0 to 1<<23-1 : 0 to 255
• uint16: 0 to 1<<24-1 : 0 to 65535
• uint32: 0 to 1<<25-1 : 0 to 4294967295
• uint64: 0 to 1<<26-1 : 0 to 18446744073709551615

Log scales §

See Logarithm

The distance from 1 to 2 is the same as the distance from 2 to 4, or from 4 to 8. Similarly 1 to 3 is the same as 3 to 9 and 10 to 100 is the same distance as 1 to 10. Thus moving a set distance along the scale means the number has been multiplied by 10 (or some other fixed factor) ;

A scale of measurement where the position is marked using the logarithm of a value instead of the actual value. Logarithmic scales reduce wide-ranging quantities to tiny scopes.

Suppose you have the inputs, which have a lot of variation:

1, 3, 5134573435345, 0.0000000053453

Taking $lo{g}_{10}$ of these numbers we get:

0, 0.477, 12.7, -8.27

which seem plottable and easily comparable. The statement “A speck of dust is half way between the size of an atom and the planet earth if you’re using logarethmic scale.” makes sense now.

Some measurements vary by a little at the small scale, or a lot at the large scale. Log scale is simply more convenient than a linear scale for these measurements. Richter Scale, concentration of ions (pH-scale), anything that involves our senses (f-stops in photography, decibels, octaves), entropy, star brightness etc. Some of these use $lo{g}_{10}$ and some use $lo{g}_2$

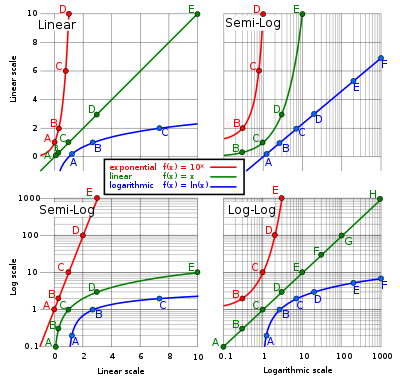
Few funny things to care about §

• There is no such thing called the exponential scale.
• Often exponential growth curves are displayed on a log scale.
• lin/linear scale is additive, while the log scale is multiplicative by a fixed number.

Other links §

• https://christine.website/blog/ln-the-natural-logger-2020-10-17

---

Growth §

This section probably has a lot of mistakes!

• OEIS Wiki Page on Growth Sequences
• Reddit post explaining the OEIS wiki page
• https://www.youtube.com/watch?v=9Bu0Hkxw88g

Growth refers to how fast a sequence of numbers increase. Sometimes decay is used to mean the opposite. Before we get more into growth, Let’s see the concept of bound. We say B bounds A (above) if B grows faster than A, that is, at some point B becomes bigger than A and stays bigger forever (the same apply for bounded below). To look at growth, we look at the derivatives.

Among other growth sequences, the most common are growth sequences that we see in the news are Linear < Polynomial < Exponential

These growths are related to respective functions, So let $t$ be a variable signifying something like time, and let $f(t)$ be some kind of function of $t$. (Informal defs., see wikipedia for formal defs.)

Linear Growth §

$f$ grows linearly if eventually, $f(t)=t$

Linear is a kind of polynomial, specifically of degree 1. Linear growth is the one most people will be familiar with, as it is everywhere in our daily life.

Exponential Growth §

$f$ grows exponentially if eventually, $f(t)=e^{at}$ for some constant $a>0$.

Other names: Proportional growth, Geometric growth(in the discrete domain)

Exponential growth refers to a pattern of growth that the rate of increase is proportional to its current value.

Polynomial Growth §

A polynomial function does not grow exponentially. An exponential function does grow exponentially. Quadratical, Cubic, Quartic,etc fall under this.

Logarithmic Growth §

$f$ grows logarithmically if eventually, $f(t)=log(t)$.

Logarithmic growth is the inverse of exponential growth and is very slow. Basically think of it like this:

• Growing from 0-10 is fastest
• Growing from 10-100 is faster
• Growing from 100-1000 is fast
• Growing from 1000-10,000 is can be slow
• Growing from 10000-100000 is can be slower
• Growing from 100000-1mn is can be slowest
• and so on.

Other Growths §

• Bounded growth
• Asymptotic growth
• Hyperbolic growth
• Logistic growth
• Iterated logarithm growth: Even slower than log growth.
• There are a lot more!

Other Links §

• A Comparison of Linear, Parabolic, and Exponential Growth
• How to read a log scale and geometric mean

---

Order of Magnitude §

An order of magnitude is an approximate position on a logarithmic scale.. Eg. $4\times 10^6$ has a common logarithm of ~6.602; Its order of magnitude is 6.

Inclusive and Exclusive §

• [ : Inclusive. Includes itself.
• ( : Exclusive. Excludes itself.

(0, 5) = 1, 2, 3, 4
(0, 5] = 1, 2, 3, 4, 5
[0, 5) = 0, 1, 2, 3, 4
[0, 5] = 0, 1, 2, 3, 4, 5

Napkin numbers §

CPU §

• 13.2ns is a couple hundred cycles

Locks §

• Laptop can Lock & unlock 61570760 times a second.
• Laptop can count to 2 billion in 1 second.
• So locks are expensive. This is second order reason why parallel is able to do shit faster.
• When we hit Amdahl’s law, need to check how split up the problem into spaces that don’t require synchronization/serialisation.

Other napkin links §

• Neurotechnology Numbers Worth Knowing