Logarithm

tags : Math, Big Oh Notation, Complexity Theory, Algorithms

Intro §

A logarithm is the power to which a number must be raised in order to get some other number. Some references refer logarithm as an exponent. It can find the cause for an effect, i.e the input for some output.

John Napier introduced Logarithm as a means of simplifying calculations in 1614, that’s about 400 years ago. It can do amazing and boring(?) things like counting zeros of a number($lo{g}_{10}(1000)=3$), extracting the fifth root of 27, list goes on. This page contains information mostly about real logs, there are something called the complex log aswell! and there’s Discrete logarithm which has uses in Cryptography.

• $y=27^{0.2}$
• Taking log on both sides
• Solving and later taking the antilog.

We can do the same for multiplying large numbers aswell.

• Convert multiplication problem into an addition problem : $lo{g}_{b}xy=lo{g}_{b}x+lo{g}_{b}y$
• Convert division problem into a subtraction problem : $lo{g}_b\frac{x}{y}=lo{g}_{b}x-lo{g}_{b}y$
• Convert exp. problem into a multiplication problem : $lo{g}_b{x}^y=ylo{g}_{b}x$

A look into the definition §

• If $x>0$ and $b\in (0,\infty ),b\ne 1$ then $y=lo{g}_b(x)$ iff $b^y=x$
• In the equation $y=lo{g}_b(x)$, $y$ is called the logarithm.
• Logarithmic functions are only defined for positive real numbers.
• The function $lo{g}_b(x)$ is continuous for $x>0$

Proving that $x$ needs to be positive is simple; If $x$ were negative or 0, $b^y$ has to result in a negative number or 0. No matter what $y$ is, since $b$ is a positive number it’s never going to be a negative number or 0.

Some interesting discussions negative base:

• Can logarithm have a negative base?
• Why must the base of a logarithm be a positive real number not equal to 1?
• Why can’t logs have negative bases? : /r/learnmath

Now why does $b$(the base) has to be a positive real number not equal to 1?

$b^y=x⟹b^{lo{g}_b(x)}=x$

Base 1 §

• For $x=5$, $lo{g}_1(5)$ has no solution.
• For $x=1$, $lo{g}_1(1)$ can be anything.

Base 0 §

For $x=0$, $lo{g}_0(0)$ can be anything, otherwise it does not have a solution. We also know that $x$ can’t be $0$

Base -2 §

• $(-2{)}^2=4$ $⟹$ $lo{g}_{-2}(4)=2=\frac{lo{g}_2(4)}{lo{g}_2(-2)}⟹lo{g}_2(-2)=1⟹2^1=-2$ which is untrue.
• It’s also because you can’t take even roots of negative numbers. Eg. $(-2{)}^{1.01}=(-2{)}^{\frac{101}{100}}=\sqrt[100]{-2^{101}}$ is not defined and we lose some properties such as continuity in the real plane.

Bases §

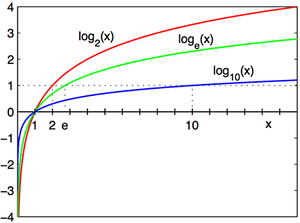
In logarithm the value of a positive number depends not only on the number but also on the base of the logarithm. There are some well known bases.

• Natural Log: $lo{g}_e$ written as ln
• Common Log: $lo{g}_{10}$ written as lg
• Binary Log: $lo{g}_2$ written as lb

Natural Log §

The natural logarithm has the number e (that is b ≈ 2.718) as its base; its use is widespread in mathematics and physics because it is immune to integration and differentiation.i.e. $\frac{d(e^x)}{dx}=e^x$. Natural log is a continuous function.

Common Log §

The logarithm base 10 (that is b = 10) is called the common logarithm and has many applications in science and engineering.

Numbers greater than 1 ($x$) §

When it’s about $lg$ of numbers greater than 1 that differ by a factor of a power of 10 all have the same fractional part. This fractional part is called the mantissa; The integer part, called the characteristic

>>> math.log10(3)
0.47712125471966244
>>> math.log10(30)
1.4771212547196624
>>> math.log10(300)
2.4771212547196626

$lo{g}_{10}$ and number of digits:

If $n$ has $d$ digits, then $10^{d-1}\le n<10^d$

$⟹d-1\le lo{g}_{10}(n)<d$ $(\because lo{g}_{10}10^y=y)$

$\lfloor lo{g}_{10}(n)\rfloor =d-1$ gives the integer part(the characteristic)

$⟹\lfloor lo{g}_{10}(n)\rfloor +1=d$, total number of digits in $n$

Numbers greater than 0 but less than 1 §

Numbers greater than 0 and less than 1 have negative logarithms for the $lo{g}_{10}$ and other usual bases; but that’s not true for something like $lo{g}_{0.2}(0.8)$

Binary Log §

The binary logarithm uses base 2 (that is b = 2) and is commonly used in computer science.

Base does not matter? §

As far as big-Oh notation is concerned, the base of the logarithms doesn’t make any real difference, because of Change of Base property and logarithms are related by some constant. So it’s common to see just $log(x)$ notation in big-Oh as the base does not matter.

$$\begin{gathered} f(x)={\int }_{-\infty }^{\infty }f\widehat{(}\xi ),e^{2\pi i\xi x} \\ ,d\xi \end{gathered}$$

$$lo{g}_b(a)=\frac{lo{g}_c(a)}{lo{g}_c(b)}$$

$$lo{g}_3(n)=\frac{lo{g}_2(n)}{lo{g}_2(3)}$$

Characteristic and Mantissa §

• Log of +ve number(2 parts)
  • Integer part: +ve, -ve or 0
  • Positive fraction: or 0

Links §

Good links §

• Learning Some Logarithms 🌟
• An Intuition for Logarithms · On the Joy of Problems

Old links §

• A Practical Use For Logarithms
• Wiki: Log
• Wiki: Natural Log
• Wiki: Common Log
• Clarify why all logarithms differ by a constant
• Level(logarithmic_quantity)
• Wiki: Super Log