Algorithms

tags : Computation and Computer Theory, Data Structures, Algorithm Problems, Recursion, Big Oh Notation, Problem solving Strategies in Algorithms

Meta §

• nlogn : we do n, logn amount of times.

Search §

Binary search §

• List must be sorted

Worst case §

• In binary search, worst case is till we half it till we can’t half no more. i.e item not in list.
• So we need to find out “How many times we can half something util we get to 1”

⇒ $\frac{n}{2^k}=1$ ⇒ $n=2^k$ ⇒ ${\log }_2(n)=k$

• i.e we can half something k times till we get 1.

About one-offs w binary search §

• The algorithm is rather simple. But there’s a solid possibility of off by one errors with implementing Binary search.
• Things mostly differ based on how low and high is defined
  • It changes the condition
  • It changes what we return
• There can be different ways to calculate low and high and all these do the same thing
  • eg. The pseudo-code in wikipedia differs from what’s there in CLRS, but they do the same exact thing.
  • It’s just about knowing what you set for low and high and then seeing that through the implementation of your algorithm. So you’ll be able to follow any implementation of binary search that way.
  • You can define this in terms of inclusive and exclusiveness.
    • $[low,high)$ : low idx from the array, high idx out of array. high is len(arr)-1
    • $[low,high]$ : low idx from the array, high idx from the array. high is len(arr)
    • In both these cases, you can come up w an algorithm for binary search but how you calculate other variables will differ based on this thing.

Integer overflow §

• We need to be careful about our invariants.
• First, high and low both need to be in the integer range that’s allowed.
• Second, the usual way of calculating mid is (high+low)/2 which is susceptible to integer overflow.
• So usually mid is calculated as low + (high-low)/2 which results in a integer that is in range and is mathematically the same as (high+low)/2. This is something we need to do due to the limitations of our computers. As mentioned here, Nearly All Binary Searches and Mergesorts are broken

Resources §

• Bitwise Binary Search: Elegant and Fast | orlp.net
• Beautiful Branchless Binary Search | Probably Dance

Sorting §

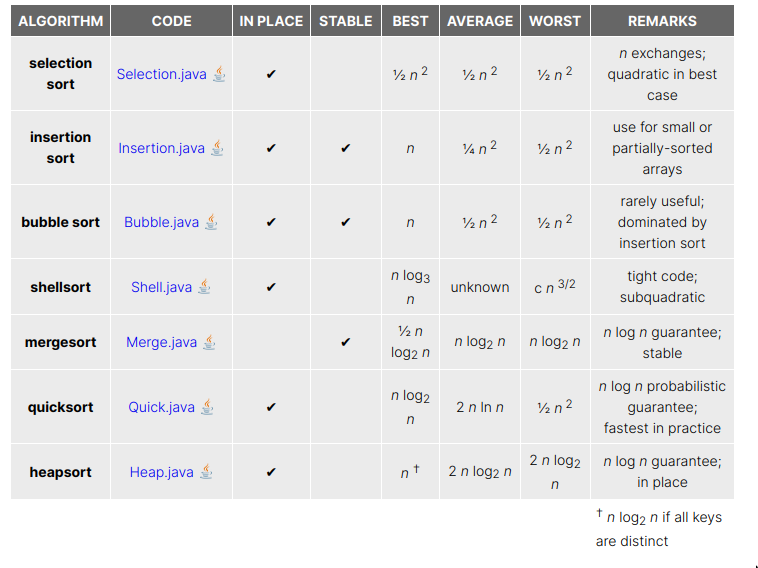
• If $X_i$ ≤ $X_{i+1}$ for the entire array, array is sorted.
• Largely two types, comparison based and non-comparison. (Lookup wikipedia). Me(a pleb) will mostly deal w comparison algorithms, non-comparison based include things like bucket sort, radix sort etc.
• Bubble, Selection and Insertion are aka Quadratic Sorting algorithms because they take quadratic time.
• stable: the stability of a sorting algorithm means if 2 elements in the input list are the same and then the list is sorted, the order of the 2 same elements will be preserved.

Exchange based §

Bubble sort §

• Repeatedly swapping adjacent elements that are out of order
• At the end of 1st pass, you’ll have the max(arr) at the end of the array

Selection based §

Selection sort §

Heapsort §

• Good to understand before Quicksort

Insertion based §

• For scenarios where they need to merge 2 lists together
• Insertion sort is very fast for small arrays and it’s also better at using the hardware than bubblesort.

Divide and Concur based §

Quick sort §

• In place sort
• Uses partitioning using pivot item
• Worst case: Reverse sorted and we pick pivot to be the smallest item.
• Time complexity: $(O(n\log n)$ , can be $(O(n^2)$ in worst case
• Implementation
  • Partition func : Produces the pivot index and moves the items from one side to other
  • Quicksort func: Calls partition func, gets the pivot, recalls itself
• If you apply quicksort to 2^20 random integers, at some point you’re sorting 2^17 8-integer subpartitions. Switching over to bubblesort for those subpartitions would be a nice optimization.
• Algo (TODO CHECK)
  • Pick a pivot.
  • Create 3 new lists
    • all elements less than the pivot
    • all elements greater than the pivot
    • all elements equal to the pivot
  • Recursively sort the first and second of these lists.
  • Concatenate the list of smaller, equal, and larger values.

Merge sort §

• For situations where you’re are getting in a piecemeal fashion. (eg. sorting a big file by loading chunks)
• Time complexity: $O(n\log n)$ (Always), but involves copying of data unlike quicksort.

Others §

Topological sort §

• https://github.com/python/cpython/blob/3.11/Lib/graphlib.py
• 7.17. Topological Sorting — Problem Solving with Algorithms and Data Structures 3rd edition

Tree Traversal §

• See Trees

Graph §

See Graphs

Pathfinding §

Meta §

• Graph search algorithms work on weighted-directed graphs
• They only understand the connectivity of the graph
• Order
  • CSS: TOP-RIGHT-BOTTOM-LEFT
  • Dir (differential direction, $(x,y)$)
    • L: [-1,0]
    • R: [1,0]
    • T: [0,1]
    • B: [0,-1]
    • LT: [-1,1] (diagonals)
    • LB: [-1,-1]
    • RT: [1,1]
    • RB: [1,-1]

Dijkstra’s shortest path §