Graphs

tags : Math, Data Structures, Algorithms, Computation and Computer Theory, Complexity Theory

Intro §

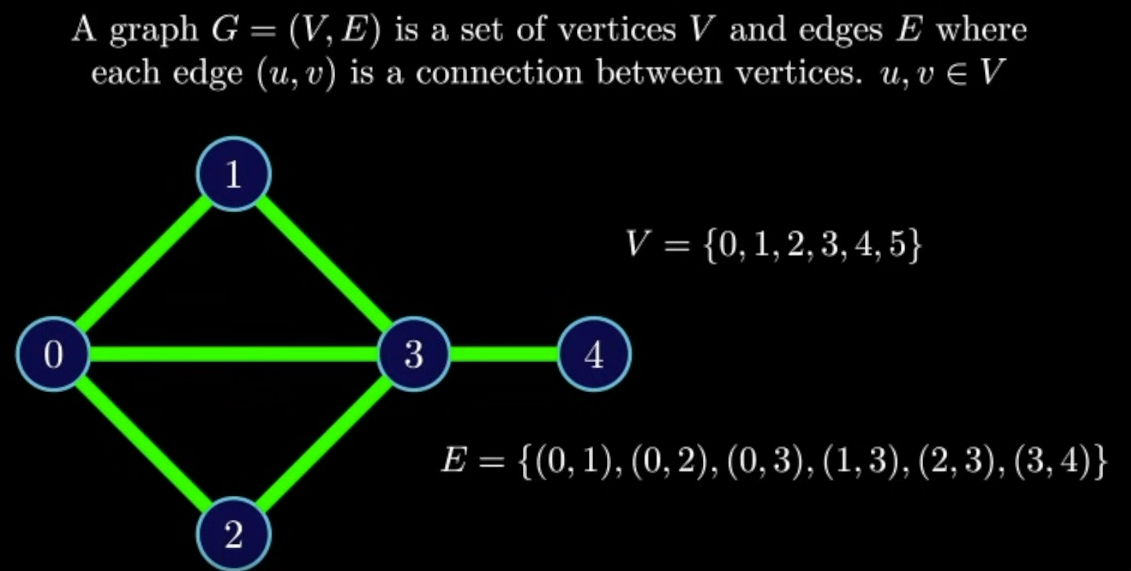
• Network that helps define and visualize relationships between various components
• Layout of the graph is not part of the graph. Following two are the same graph
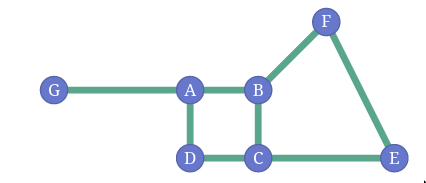
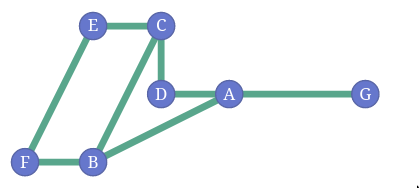
• You can define different networks in the same data. Some networks are more useful than others.
• Possible use
  • Can be used in infinite ways. If you can make your data look like a graph, you can reuse a wide variety of graph algorithms.
  • Eg. You could represent your game’s economy as a graph, with wheat and bread as nodes and baking as an edge.
  • Introduction to Behavior Trees | Game tree | State Game Programming | Polygonal Map Generation
  • Graphs and networks | plus.maths.org

Basic terms §

• $0(V\text{*}E)$ means that we will check every vertex, and on every vertex we check every edge
  • $V$ / Node : Set of vertices
  • $E$ / Edge : Set of edges, connection btwn nodes
• Path: Sequence of vertices connected by edges
• Connectivity
  • Verted:Connected: 2 vertices are connected is there’s a path connecting them
  • Graph:Connected: When every node has a path to another node
  • Connected Component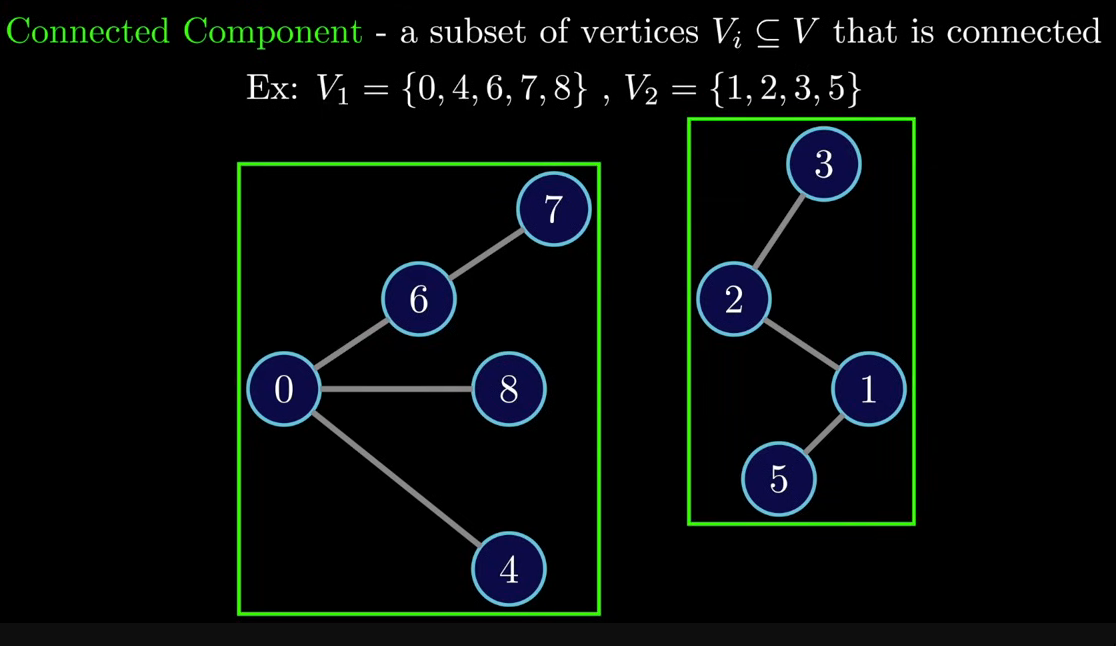

Common problems §

• Does a path exist
• Is the graph connected
• What’s the shortest path
• Does it contain cycle
• Given a set of k colors, can we assign colors to each vertex so that no two neighbors are assigned the same color? (Sudoku problem)
• Does a path exist that uses every edge exactly once?
• Does a path exist that uses every vertex exactly once? (NP Hard, See Complexity Theory)
• Solving the minimum cut problem for undirected graphs | Hacker News

Flavors §

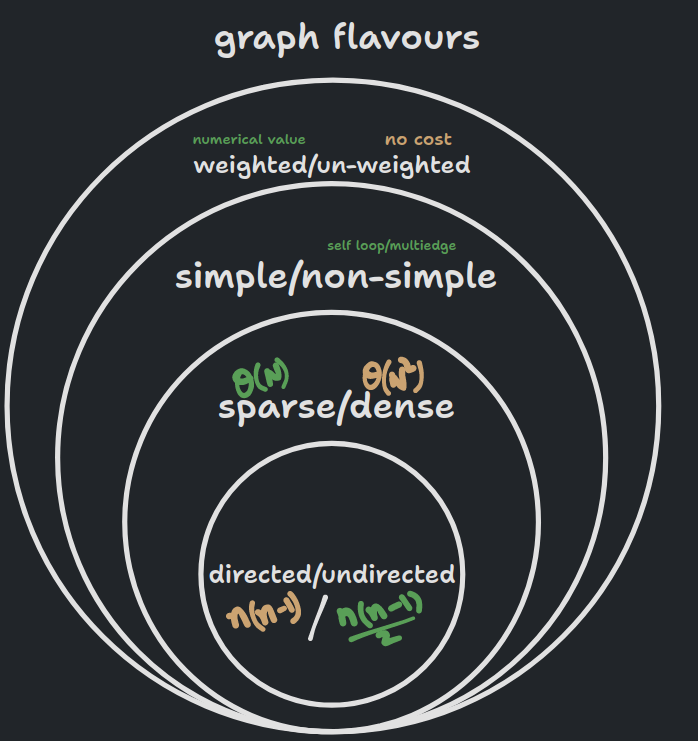
• In the diagram, $n(n-1)$, $n(n-1)/2$ is the max number of edges.

Cycle §

Cyclic §

• Path that starts and ends in the same vertex. All Cycles are Path, but not opposite.
• A graph can have multiple cycles
• When you start at Node(x), follow the links, and end back at Node(x)
• Needs 3 nodes
• Odd/Even cycles
  • odd : odd no of vertices in the cycle
  • even : even no of vertices in the cycle

Acyclic §

A graph that contains no cycles

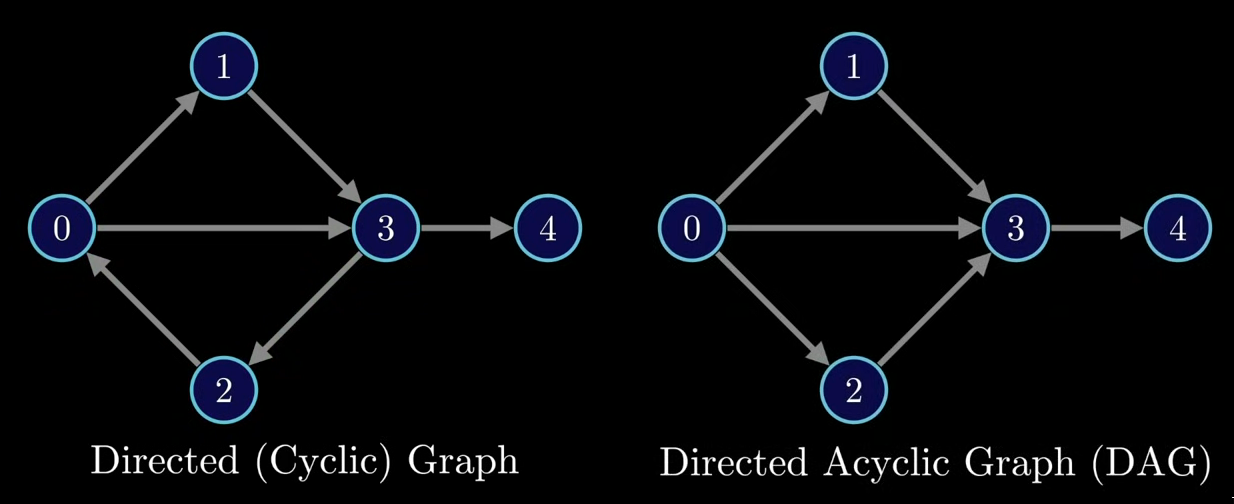
DAG §

Directed, acyclic graph.

Partite §

k-partite §

• A graph whose vertices are (or can be) partitioned into k different independent sets.
• Recognition of $k>2$ is NP-complete

2-partite (bipartite) §

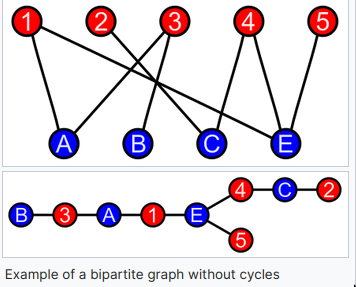
• aka 2-colorable
• If there exists and partition of the vertex set into two disjoint-sets
  • i.e $V_1$ has no adjacent vertices & $V_2$ has no adjacent vertices
  • If they’re adjacent then one of them is in $V_1$ and other one is in $V_2$
• Bipartite graphs may be recognized in polynomial time
• Bipartite graphs cannot have any odd cycles. i.e odd cycles not allowed.
  • Eg. triangle has 3 vertices, and is a cycle. So triangle is not bipartite.
• How to Tell if Graph is Bipartite (by hand)

• Types

  • Complete: Every vertex in one set is connected to every vertex in the other set.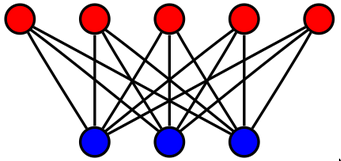
  • Matching: Each vertex is connected to at most one other vertex from the opposite set.
  • Planar: Can be embedded in the plane without any edges crossing.

• Links and resources

  • Proof: If a Graph has no Odd Cycles then it is Bipartite
  • Vertex Colorings and the Chromatic Number of Graphs

Others §

• Regular: Every vertex has the same degree.
• Multigraph: Allows multiple edges between the same pair of vertices.
  • Eg. Being able to swim across a river or take a raft across the same river is an example in games.

Graph representation §

Adjacency Matrix §

• $G=(V,E)$ with $n$ vertices and $m$ edges
  • $M$ is a matrix with $n\text{texttimes}n$
  • $M[i,j]=1$ if $(i,j)\in E$
  • $M[i,j]=0$ if $(i,j)\notin E$
• Space complexity is $(O(n^2)$
  • Has entry for no-edges
  • Has double entry for undirected edges

Adjacency List §

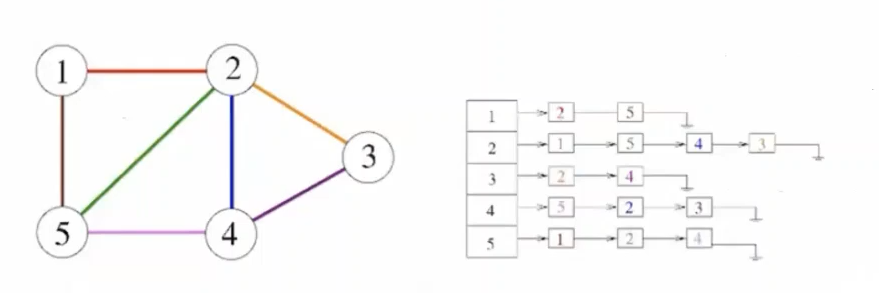
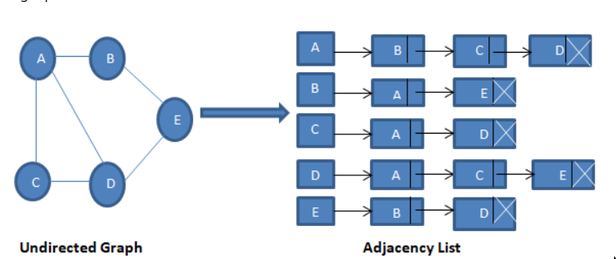
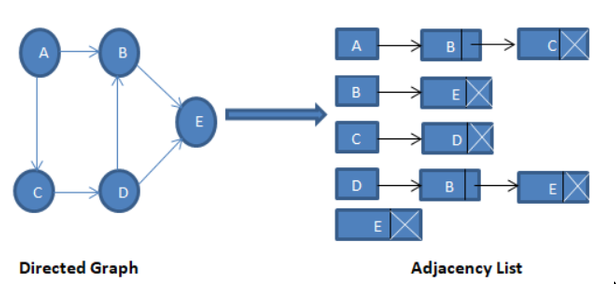
• Nx1 array of pointers
• Each element(vertex($i$)) points to a linked list of edges incident on vertex $i$
• The direction/order of items in the “edge list” for each “vertex” do not tell anything about if there any network exists between a edge items themselves.
  • i.e A: [B, C], this means A is connected to B and C but tells us nothing about the relation of B and C. This can be confusing because B and C are next to each other in a link list. In other words, link list is just the implementation and not the logical view.
• List contains list of “what am i adjacent to”
• Each vertex (N) has set of edges (M). No of edges per vertex is called the degree
  • So, in a way no. of neighbors of some vertex is the degree
• Space complexity
  • Sparse
    • Space Complexity
      • $\theta (N+2M)=\theta (n)$ (undirected) or $\theta (N+M)=\theta (n)$ (directed)
      • total N vertices (items in array)
      • total M edges
      • In undirected, each connected N has the edge mentioned both ways. So 2M
  • Dense
    • Space Complexity: $\theta (N\text{*}N)=\theta (n^2)$

Graph Nodes §

• Graph Nodes etc. like we do with linked list
• But we don’t do it this way in practice generally

Links and resources §

• Matrices and Graph | Hacker News

Viz §

• https://visualgo.net/en/graphds
• https://www.cs.usfca.edu/~galles/visualization/DFS.html