tags : Data Structures, Graphs
Tree Traversal
Meta ideas about tree traversal
- We usually just go L -> R
Complexity
- All trees have
n - 1edges,nbeing the number of nodes. - Time complexity:
O(V + E)⇒
About {in,pre,post}order
- BFS doesn’t have
{in,pre,post}order, those are DFS specific. {pre,post}orderwork forn-arytrees, while inorder becomes a little weird for anything that’s not a binary tree.
Recursion and traversal
| BFS (Queue) | DFS (Stack) | |
|---|---|---|
| Recursive | Not natural | Yes, that’s the way. Preserves shape/structure. |
| Iterative | Yes, that’s the way | Unsual to do, might help w limited call stack |
DFS (Stack)
- Workhorse: push and pop things on a
stack(call stack)
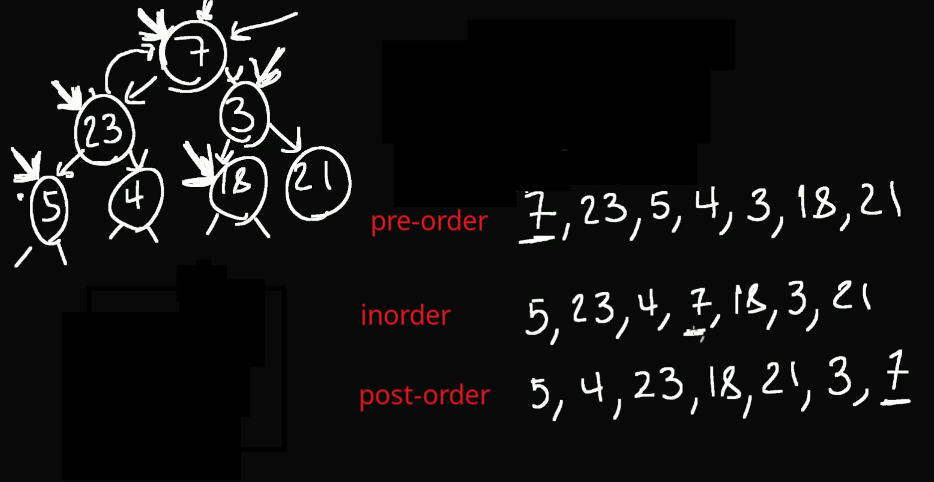
Preorder
VisitNode() + RecurseL() + RecurseR()- Root’s in the beginning
Inorder
RecurseL() + VisitNode() + RecurseR()- Root’s in the middle
- Inorder traversal of a Binary search tree will print things in order
Postorder
RecurseL() + RecurseR() + VisitNode()- Root’s in the end
Implementation
- Recursive
- DFS uses a stack to maintain a frontier, and recursion has an implicit stack (call stack)
- Implementing DFS using recursion simply means replacing the stack with a call stack.
- Iterative
- To convert it into an iterative DFS you can simply use an actual stack data structure, but you now need to manage the stack yourself.
BFS (Queue)
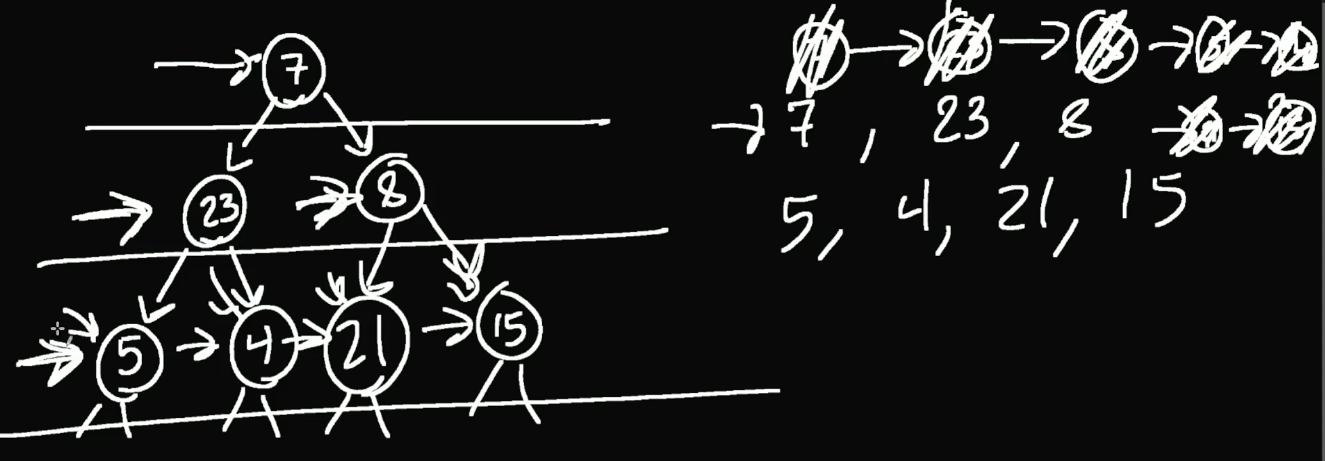
- Workhorse: enqueue and dequeue things on a
queue(auxiliary storage)
while !q.empty?
curr = q.rm_from_start() // dequeue
print(curr) // do whatever w curr
q.enqueue(curr.l)
q.enqueue(curr.r)Implementation
- Mostly uses a queue
- BFS and recursion cannot be combined as naturally since BFS does not use a stack
Tree based Structures
Basic definitions
- Root: the most parent node. The First. Adam.
- Height: The longest path from the root to the most child node
- Leaves: a node without children
- Branching factor: the amount of children a tree has
- General tree: A tree with 0 or more children
- Binary tree
- A tree in which has at most 2 children, at least 0 children
- Each level in a binary tree is approx. half the size of the entire tree above it.
Tree ADTs
Binary search tree (BST)
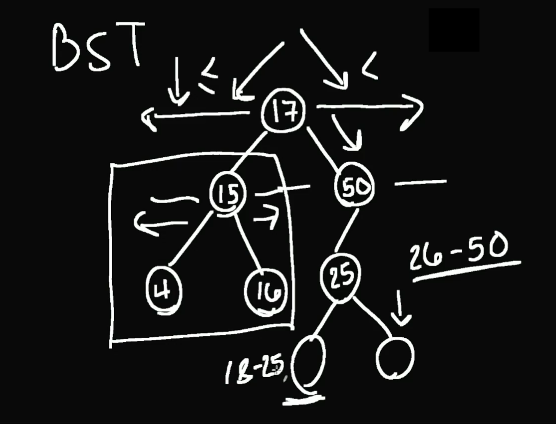
- Rule at every node: Left ≤ Node < Right (Similar to Quicksort)
- A tree in which has a specific ordering to the nodes and at most 2 children
- In-order traversal will result in an ordered list
-
Search
- Searching: Searching is similar to Binary search
- Time Complexity: - . in the case where the BST is simply a linked list. i.e How balanced your BST will determine the complexity.
-
Insertion
- Insertion inherently un-balances the tree
-
Deletion
- Choose
smallest on large-sideorlargest on small-side.- We can choose any but if we have the
individual heightof the node, we can make a better decision as we’ll know which one to choose and shrink our tree.
- We can choose any but if we have the
- Then replace the parent to be removed with it.
- Choose
Heap/Priority Queue
- Heap is an implementation of a Priority Queue ADT
- There’s usually no need to traversing the tree as you only look at the top for priority
- A
binary treew constraints:- Every child and grand child is smaller (MaxHeap) than current node
- Every child and grand child is larger (MinHeap) than current node
- i.e Root node is at some extreme
- Self balancing
- Every level of the tree is complete
- Whenever a node is added, we must adjust the tree
- Whenever a node is deleted, we must adjust the tree
-
Array Implementation
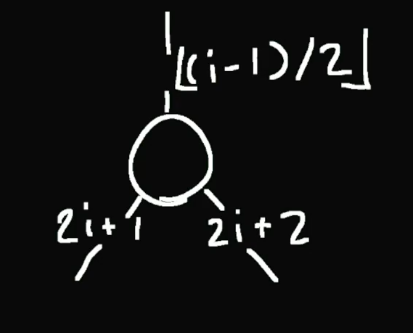
- Heap-ordered binary tree Implementation
-
Binary Heap
- Binary heaps are a common way of implementing priority queues
- The Data Structures used for
Heapsort
Tries/Prefix Tree/Re’trie’val tree
- Used for auto-completion/caching type stuff
- Value is usually a string
-
Complexity
- You need to think about what
nis. - The complexity of creating a trie is O(W*L), where W is the number of words, and L is an average length of the word: you need to perform L lookups on the average for each of the W words in the set.
- Same goes for looking up words later: you perform L steps for each of the W words.
- If the longest english letter is 12, then it’s 12 node check. That’s constant time.
- In this case
nis the height and the height is bound by the en dictionary. - So trie is good for cases where you can determine the height in advance
- You need to think about what
Balanced tree
- Depth is uniform across the entire tree.
- perfectly balanced when any node’s left and right children have the same height.
- There are different ways to balance a tree. Popular rotation techniques are AVL and RB trees.
- RB : If I don’t find things often but I insert a lot. (Fast balancing)
- AVL: If I find a lot but insert rarely. (Slower balancing)
- Object-Oriented Design and Data Structures
Merkle Tree
Skip List
B-tree / Btree
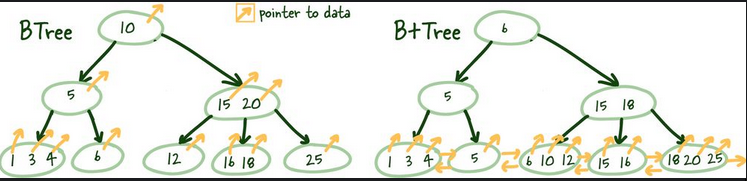
- B-Trees and Database Indexes | Hacker News 🌟
- Binary Search Tree(BST) vs B-tree
- B-Trees: More Than I Thought I’d Want to Know | Ben Congdon
- Relational database on top of key-value store explained (or why B-trees are cool) - Gregory Trubetskoy
- The Taming of the B-Trees - ScyllaDB
- It’s a data structure that aims for “read and write large blocks of data”,
- Key point is that such trees usually grow wide and shallow, so for some type of query (remember, it’s still a search tree) only very few nodes are to be “touched”.
- This is important, because such access could be very expensive (think of rotating HDD).
B+ tree
- The subtleties of proper B+Tree implementation | Hacker News
- B+ Tree Visualization | Hacker News
- B+tree is a variant on B-Tree
- The main difference B+ Trees show off is that intermediate nodes don’t store any data on them. Instead, all the data references are linked to the leaf nodes, which allows for better caching of the tree structure.
- Secondly, the leaf nodes are linked, so if you need to do an index scan, you can do a single linear pass rather than traversing the entire tree up and down and loading more index data from the disk.
LSM Tree / LSMT
-
LSMT in Database
- The Log-Structured Merge-Tree (LSM Tree) | the morning paper
- Intro into database storage engines
- LSM tree normally has an in-memory sorted list of key-value pairs called a MemTable. Writes are inserted into this MemTable. To keep writes durable, writes are also sent to a write-ahead log (WAL). When MemTables get large, they’re frozen (made immutable) and flushed to disk as sorted-string tables (SSTs). (from materializedview blog)
- Allows different storage(write) and access(read) characteristics.