Recursion

tags : Math, Programming Languages, Automata Theory, Tail Calls

FAQ §

Recursive procedure vs Recursive process §

Knowing the procedures and not knowing the process is similar to someone who has learned the rules for how the pieces move in chess but knows nothing of typical openings, tactics, or strategy. - 1.2

Procedure §

• A procedure is a pattern for the local evolution of a computational process.

Process §

• Recursive: Needs to maintain the state of the caller while the recursive call is in progress.
• Iterative: The earlier state can be discarded.

Why does this distinction matter? §

• This is commonly used in functional programming, a recursive procedure is used to do a iterative process in the absence of loops in the language.
• This came to my mind when I thought of implementing BFS recursively. This is like trying to draw a square circle. It’s not a recursive process and yet I wanted to do it recursively, I could probably do it but at the end it’ll probably just the procedure that’ll be recursive and not the process by the nature of the problem.

Premitive Recursive Functions §

• https://www.nayuki.io/page/primitive-recursive-functions
• https://matklad.github.io/2024/08/01/primitive-recursive-functions.html

Stack contains Frames §

• Stack
  • Stack aka call stack. Stack grows downwards. Stack contains frames.
• Frame
  • Frame aka Stack frame.
  • Frame = function arguments + local data + return address
  • Each call to a function creates a new frame and pushes it into the stack

JMP vs CALL §

These are assembly instructions but do not directly related to recursion/tail recursion but good to keep in mind.

• JMP : A transfer of the control to another location and the control does not automatically return to the point from where it is called.
• CALL CALL pushes the current instruction pointer on the stack and then then JMPs to the location

Recursion and the Stack §

• Generally, programming Languages use the call stack to implement recursion.
• So if you do $n!$ of a large number, there’s solid chances you’ll blow off the stack.
• But if get to program in a language that supports tail recursion (essentially iteration), usually you’ll get infinite recursion without a stack overflow :)
• See Recursive tail calls

What? §

• Function that calls itself until the problem is solved.
• Involves what is referred to as a “base case.”
  • A base case is the point in which the problem is solved at.

Factorial example §

foo(n):
    if n = 1:
       return 1 // base case
    return n*foo(n-1) // inductive case

When to use? §

• When it’s too difficult/cumbersome to do iteratively
• When there’s high degree of branching factor

Parts §

This base and inductive cases are more for understanding, when implementing things usually get mixed more or less.

Base case §

• Solve the simplest cases in the base case
• The base case does not have to be just one single condition. It can be multiple conditions.
• Preferably move checks and validation sort of things to the base case. But this is not a rule.

Inductive case §

• Sub parts (all may not be at use)
  • pre-operation : Before you recurse
    • useful when we want to recurse but also do some comparison of sorts on the result before recursing. Eg. find max in a list
  • recurse : Where you recurse
  • post-operation : After you recurse but before the final return. (i.e there can be early returns elsewhere)
    • useful when we want to modify the recursed value

Types §

Position §

Head §

• Without a pre-operation

Middle §

• w a pre-operation and post-operation

Tail §

See Tail Calls

Number of calls §

Linear §

Only a single recursive call in the function

Non Linear §

• AKA Multi/Exponential recursion

• General Non-Linear Recursion

  • >1 recursive calls in the function
  • Binary recursion is a subset of this w 2 recursive calls

• Tree/bifurcating Recursion

  • Divide the input into parts
  • Call the recursive function on each part

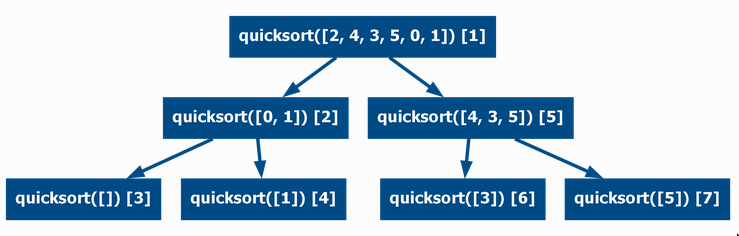
• Nested Recursion

  • One of the arguments to the recursive function is the recursive function itself

Function called from §

Direct Recursion §

• Function calling itself

Indirect/Mutual Recursion §

• Function calling another function calling the initial function
• Two function calling each other

Nature §

This is about where a recursive procedure gets the input and how it processes that input. But this doesn’t really matter much. But good to know.

Structural §

• A recursive call is made on a subset of the original input data
• The term “structural recursion” comes from the fact that these structures (lists, BSTs, etc.) can be defined recursively.
  • You are “undoing” the operation from which these structures are built out of one another.
  • Eg. A list is either nothing, or a cell followed by a list.
  • Eg. A binary tree is either nothing, or a node with two binary trees as children.

Generative §

• A recursive call is made on data that was constructed/calculated from the original input data.
• w Generative recursion, there’s no no guarantee that it terminates.
• Eg. In quicksort we create some auxiliary data structures from the original input.

Optimizations for recursion §

Memoization §

• Cache repeated recursive calls

Tail call optimzation §

See Tail Calls

Trampolining §

from __future__ import annotations
 
from typing import TypeVar, Callable, TypeAlias
 
T = TypeVar("T")
TrampolineFunction: TypeAlias = "Callable[[], T | TrampolineFunction[T]]"
 
def trampoline(function_or_result: T | TrampolineFunction[T]) -> T:
    if not callable(function_or_result):
        return function_or_result
 
    while callable(function_or_result):
        function_or_result = function_or_result()
 
    return function_or_result
 
def fibonacci(
    n: int, partial_result: int = 0, result: int = 1
) -> int | TrampolineFunction[int]:
    if n == 0:
        return 0
    if n == 1:
        return result
 
    # NOTE: Here we're returning lambda instead of a recursive function
    # NOTE: The outer function, "the trampoline" will handle the result and
    #       decide what to do
    return lambda: fibonacci(n - 1, result, partial_result + result)
 
assert str(trampoline(fibonacci(10000))).startswith("3364476487")

• Idea is to not make the final continuation call inside the function, but to exit and to return the continuation to a trampoline.
• That trampoline is simply a loop that invokes the returned continuations.

Tips from the Internet §

• stop trying to imagine the flow, you’ll just get lost and more confused.
  • Instead, start with your inductive case
    • If someone handed you the answer to a smaller problem, how would you get the answer to your problem?
  • Once you’ve figured that out, switch to the base case
    • What are the smallest problems that you can solve immediately?
  • Put the two together and you’re probably 95% of the way there.
• Understand
  • The difference between structural and generative recursion
  • The relationship between structural recursion and induction
    • Every structurally recursive function is a mirror of an inductive definition.
• The biggest mistake one can make is writing a recursive function without thinking about the inductively defined data it works on.

Practice tips §

• pick 10-20 string or array functions out of your favorite language’s standard library and reimplement them without loops.