Parsers

tags : Programming Languages, Context Free Grammar (CFG), Parsing Expression Grammar (PEG)

Types §

Top-Down Parser §

• From the root and move down to the tree’s leaf.
• Sees a source code, which contains functions, which contains expression.
• Eg. Recursive Descent Parser(handwritten) and LL(1) parsers, example of Recursive Descent parser for Ruby

Bottom-Up Parser §

• From leaves to the tree’s root.
• Sees expression, which belongs to functions, which results the full source.
• Eg. LR parser, SLR parser, CLR parser, etc.
• Can be implemented using backtracking, but mostly uses some shift-reduce sort of algorithm

High level steps/concepts §

Inputs and Outputs §

Input §

• Stream of tokens from a Lexer

Output §

• parse-tree?: Not really, you can evaluates arithmetic expressions in-line with the parse. Subexpression is immediately evaluated, no tree is built.
• parse tree traversal?: Probably. It gives us a way we’d traverse the tree.
  • Polish and Reverse Polish notation fully encode a tree structure and the steps you would take to traverse it.
  • While we can get a tree, we don’t really need to do that always
  • Because it gives a way to traverse, we can consume the output of the parser while parsing happens without generating the whole tree!
• But if you think about it, the parser just adds a bunch of structure that is defined on top of the sequence of input tokens. i.e The leaf nodes are always exactly the input tokens themselves, in exactly the order of the input.
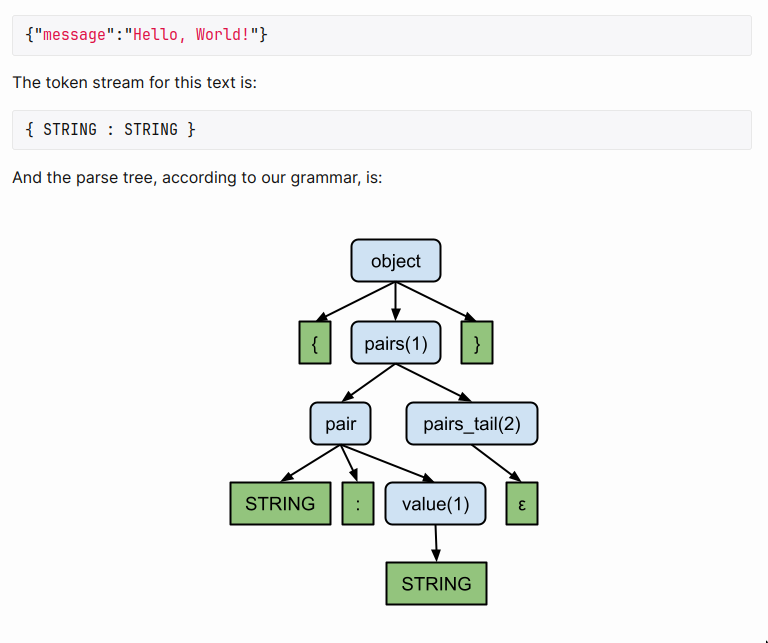
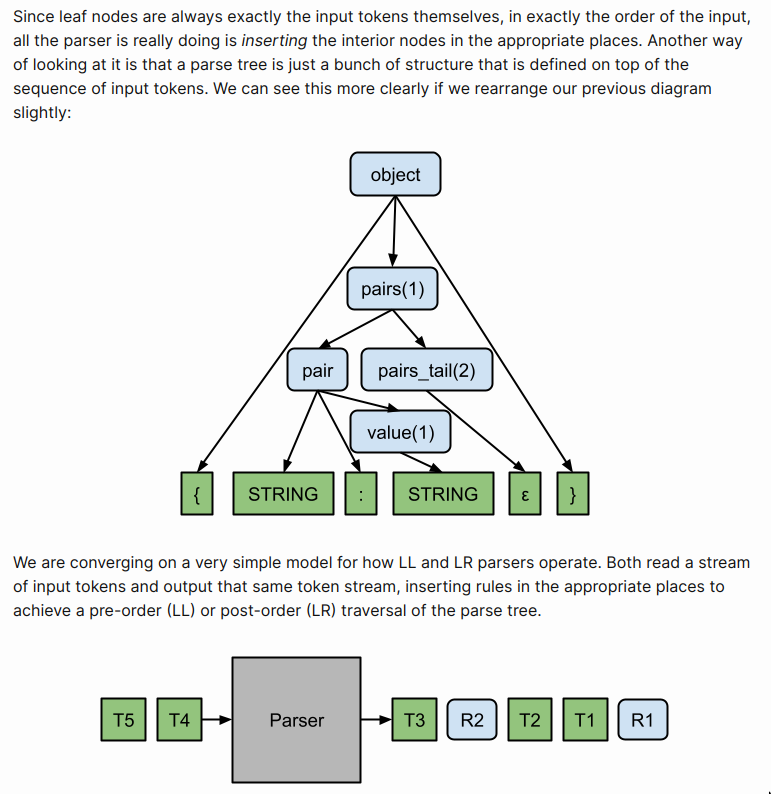
• So in a very reduced manner, we can say parsers output a stream of tokens with rules added to appropriate places giving us pre/post-order traversal.

LL vs LR §

• LL parser outputs a pre-order traversal of the parse tree
  • Produces a left most derivation
  • Topdown
  • Predictive parsers
• LR parser outputs a post-order traversal of the parse tree
  • Produces a reversed rightmost most derivation
  • Bottomup
  • Shift reducers parsers

In Practice §

• Not all parsers are purely based on formalism.
• Usually hand-written parsers are not based on any formalism at all.
  • Language specifications are often defined in terms of a formalism like BNF
  • But it’s almost never the case that real parsers can be generated directly from this formalism.
  • Eg. GCC moved away from their Bison-based parser to a handwritten recursive descent parser. So did Go. While some notable language implementations do use Bison (like Ruby and PHP), many choose not to

Parsing techniques §

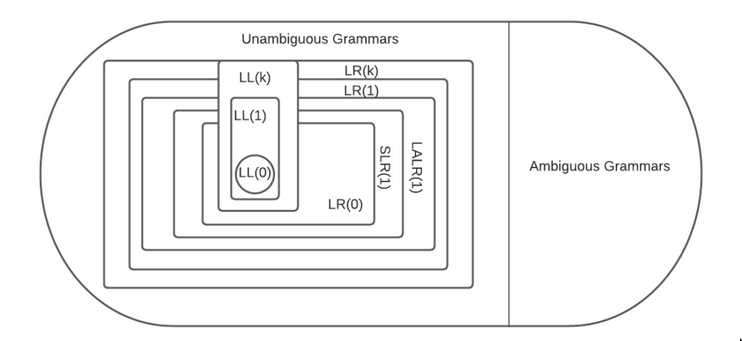
• See Parsers
• Different parsing techniques can deal with different subsets of CFG (Some of these parsing techniques are beyond CFG too)
• Each of these techniques have their own set of algorithms that implement them. Eg. The Operator Precedence Parser uses the Shunting yard algorithm
  • “LL parser” and “LR parser” are not actually specific algorithms at all, but rather generic terms referring to families of algorithms.

Classification (non-exhaustive) §

• TD: Top Down, BU: Bottom Up
• A: Active, P: Passive
• OP: Operator Precedence
• PS: Push, PU: Pull
• TD: Table Driven
• INC: Incremental
• PR: Predictive

Technique	Type	Subset	Use/Example
Chart Parser	{TD/BU}+{A/P}+INC	All of CFG
Earley	Chart Parser (TD)	All of CFG
CYK Algorithm	Chart Parser (BU)	All of CFG
GLR	Shift Reduce	All of CFG	Tree-sitter
Shift Reduce	BU+TD
LR(k)	Shift Reduce	LR(k)
Simple Precedence	Shift Reduce	Simple Precedence Grammar LR(1)
Operator Precedence	Shift Reduce+OP	Operator Precedence Grammar	Calculators
Packrat	Shift Reduce	PEG
Recursive Ascent	Shift Reduce (Recursive LALR)
LL(k)	TD+PR	LL(k)
Recursive Descent	TD+PR	Not limited to CFG, TDPL
Pratt	TD+OP

Earley Parser §

Shift Reduce §

• table driven, bottom up parsing
• LR parsing and its variations are shift-reduce
• Simple Precedence Parsers are also shift-Reduce
• Operator Precedence Parsers are also shift-Reduce
  • Can produce either a postfix notation string/RPN or an abstract syntax tree (AST)
• Steps
  • shift: add this token to the stack for later reduction
  • reduce: pop tokens from the stack and form a syntactic construct
  • end, error: no known rule applies
  • conflict: does not know whether to shift or reduce

Recursive Descent §

• Real language grammars are hardly neatly classified into LL, LR et al. Hence the vast majority of languages today use handwritten adhoc Recursive Descent parsers.
• Can be directly encoded in the host language
• It can parse more than CFG. TDPL grammar can be viewed as an extremely minimalistic formal representation of a recursive descent parser
• The Recursion in “recursive descent” happens when the parser “descends” into a nested rule.

Packrat §

• A form of parser similar to a recursive descent parser in construction
• Except during the parsing process it memoizes the intermediate results of all invocations of the mutually recursive parsing functions
• Ensuring that each parsing function is only invoked at most once at a given input position
• Takes Parsing Expression Grammar (PEG) instead of LL

Recursive Ascent §

• Uses mutual Recursion instead of parser tables for LALR parsing
• Can be directly encoded in the host language
• Writing a recursive ascent parser by hand - Abubalay

LL(k) §

• (L)eft-to-right, (L)eftmost derivation, (k) lookahead
  • Parses the input from left to right
  • Performing leftmost derivation of the sentence
  • With k token of lookahead
• Usually LL refers to LL(1)
• Converts input grammar into parser tables OR can be parsed recursively

LL(1) §

• The traditional approach to constructing or generating an LL(1) parser is to produce a parse table which encodes the possible transitions between all possible states of the parser.
• Such CFG can be converted into Pushdown Automata (PDA)

Programming Languages and LL(k) §

• Most Programming Languages have LL(1) grammars, they are never ambiguous. (They need to be unambiguous for what they do)
• Not all programming languages can be parsed with LL(1). Some languages are designed for easy parsing, some grow adhoc.
  • C : You need an LR(1) parser for it.
  • C++ : You need a GLR/Earley/etc. parser to parse it (although gcc/clang use a recursive descent parser with some cool tricks)

Conflicts §

• first/first set
• first/follow set

LR(k) §

• (L)eft-to-right, (R)rightmost derivation, (k) lookahead
• Donald Knuth invented the LR parser (?)
• All LR(k) grammars can be mechanically transformed into LR(1) grammars, with the consequence that there are only two categories of LR languages: LR(0) and LR(1)
• Converts input grammar into parser tables

Variations §

Variants	Description
LALR	Look Ahead LR, Simpler than LR(1)
SLR	Simple LR, Simpler than LR(1)
CLR	Canonical LR, canonical name for the LR(1) parser
GLR	Generalized LR, Can handle ambiguous grammar

Pratt Parsing (TDOP) §

• Top down operator precedence (TDOP) parser
• An enhancement of recursive descent parsing algorithm
• Uses the natural terminology of precedence and associativity for parsing expressions, instead of grammar obfuscation techniques.
• Resources
  • Simple but Powerful Pratt Parsing
  • TDOP / Pratt parser in pictures
  • Pratt Parsers: Expression Parsing Made Easy – journal.stuffwithstuff.com
  • Pratt Parsing Index and Updates

Related Concepts §

Parsing related trees §

Concrete Syntax Tree (CST) / Parse tree §

Grammar	Parse Tree
Transformational Generative Grammar	Phase Markers
Phrase structure grammar	Constituency-based parse trees
Dependency grammar	Dependency-based parse trees

• See Parse Tree
• Reflect the syntax of the input language

Abstract Syntax Tree (AST) §

• The syntax is “abstract” in the sense that it does not represent every detail appearing in the real syntax, but rather just the structural or content-related details.
• Eg. For instance, grouping parentheses are implicit in the tree structure, so these do not have to be represented as separate nodes.
• An AST usually contains extra information about the program, due to the consecutive stages of analysis by the compiler.
  • Eg. it may store the position of each element in the source code, allowing the compiler to print useful error messages.
• Since the language parsed by the parser is usually more than context-free and falls in the realm of context-sensitive
  • AST helps in terms of it allows you to add that context. Eg. allows new types to be declared, duck typing, operator overloading etc.
• Semantic Analysis
  • AST is used intensively during semantic analysis, where the compiler checks for correct usage of the elements of the program and the language.
  • The compiler also generates symbol tables based on the AST during semantic analysis.

Parse table §

• Encodes the possible transitions between all possible states of the parser.

Online and Offline §

• online: It consumes the input tokens in a specific order and performs as much work as possible after consuming each token
  • Can start producing output while they are still consuming input.
  • Both LL and LR are online parsers because of lookahead

Predictive §

• Predictive parsing is parsers that do not require backtracking
• Predictive parsing is possible only for the class of LL(k) grammars

Generators/Tools §

Parser Generators §

• A parser generator reads in a grammar and spits out a parser.
• It is generally not possible to combine existing grammars into a new grammar
• They may be rigid in where you put the border between lexical and grammatical analysis, between grammatical and semantic one
• Examples
  • ANTLR
    • ANother Tool for Language Recognition
    • A parser generator for efficient LL(k) parsers, where k is any fixed value.
    • Can generate code in more languages than Bison
    • ANTLR 4 deals with direct left recursion correctly
  • Bison
    • Can generate LALR(1), LR(1), IELR(1) and GLR parsers
• See Bison
• Comparison of parser generators - Wikipedia 🌟
• Parser generators vs. handwritten parsers: survey
• There are so many better options these days, you’d be mad to use Flex and Bison.

Parser Combinators §

A combinator is, classically speaking, a function which takes functions and returns functions.

• Only Accepts several parsers as input and returns a new parser as its output.
  • Here parser is a function accepting strings as input and returning some structure as output, typically a parse tree
• Parser Combinators let you build parsers easily, just by specifying the grammar.
  • Sometimes they let you specify the grammar in a way it looks like normal code
  • Sometimes they might also allow to use some special grammar notation
• Eg. Parsec

FAQ §

LL vs LR §

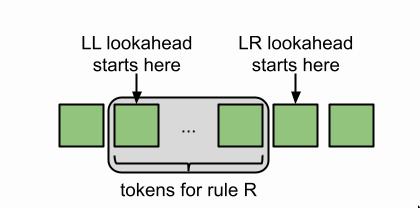
• There is no LL(0) parser, LL’s need a lookahead.
• LR parsers(LR(0)) can do without a lookahead because LR’s lookahead starts from the back and it gets to see all of the rule’s tokens.
• Since LR lookahead starts from the end of a rule, a LR(1) parser has strictly more information available to it when making a decision than an LL(1) parser.
• LR parsers can handle left recursion

Resources §

• LL and LR in Context: Why Parsing Tools Are Hard
• Resilient LL Parsing Tutorial