Context Free Grammar (CFG)

tags : Chomsky Hierarchy, Regular Expressions, Automata Theory, Parsers

A context-free grammar is a grammar in which the left-hand side of each production rule consists of only a single nonterminal symbol.

2 non terminals, CFG sad :)

$$L(G)=a^n{b}^n{C}^n|n\ge 1$$

1 non terminals, CFG go brrr :)

$$L(G)=a^n{b}^n|n\ge 1$$

What? §

• Introduced in the Chomsky Hierarchy, one of the few types of grammar. Type 2 to be specific.
• Recursive system for generating strings
• Almost every programming language defines its language using CFG using the BNF notation, but most languages are actually context sensitive

Grammar §

• terminals
  • symbols of the alphabet of the language being defined.
• variables
  • nonterminals: A finite set of other symbols(strings), each of which represents a language.
  • Recursive sets of strings (languages)
  • Start symbol
    • The variable whose language is the one being defined.
• rule: Referred to as a production
  • head -> body
  • variable (head) -> string of variables and terminals (body)

Derivations §

• Derivations allow us to replace any of the variables in the string.
  • any is key here, it’s what makes things context free
• We derive strings in the language of a CFG. So we can have many different derivations of the same string
  • Starting with the start symbol
  • Repeatedly replacing some variable A by the body of one of its productions.
  • i.e, the productions for A are those that have head A.

Parsing CFG §

Parse Tree §

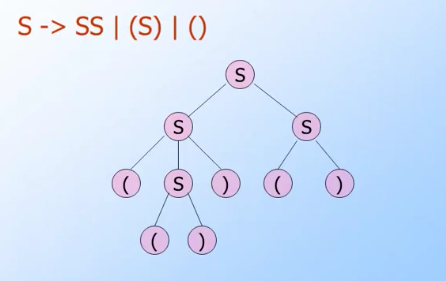
• Trees labeled by symbols of a particular CFG.
• Leaves: labeled by a terminal or ε
• Interior nodes: labeled by a variable or ε.
  • Children are labeled by the body of a production for the parent.
• Root: must be labeled by the start symbol.
  • If root is not a start symbol, we call it “Parse Tree w root A” (A being some arbitrary variable)

Ambiguity and Un-Ambiguity §

Ambiguous Grammar §

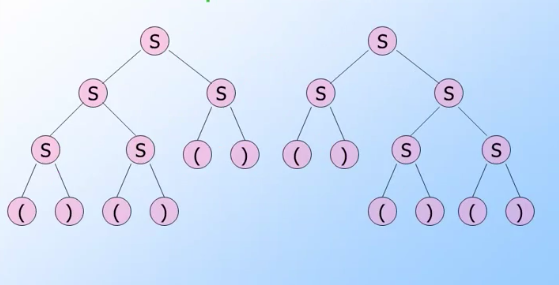
• A CFG is ambiguous if there is a string in the language that is the yield of two or more parse trees.
• There is a string in the language that has 2 different leftmost derivations.
• There is a string in the language that has 2 different rightmost derivations.

Un-ambiguous §

• Some ambiguous grammar can be made un-ambiguous grammar but some grammars are inherently ambiguous.

Parsing techniques §

See Parsers

Grammar Specification Types §

• See BNF
• Extended Backus–Naur form (EBNF)
• Augmented Backus–Naur form (ABNF).

Derivation §

Expression types / Expression notation §

• Polish and Reverse Polish notation, as they are usually described, do require that all operators have a known arity.
• Arity is just the number of operands that the operator takes.
• This means, for example, that unary minus needs to be a different operator than subtraction. Otherwise we don’t know how many operands to pop from the stack when we see an operator.

1 + 2 * 3  // Infix
+ 1 * 2 3  // Polish (prefix)
1 2 3 * +  // Reverse Polish (postfix)

Prefix §

• AKA Polish Notation

Infix §

“writing grammars for infix arithmetic expressions isn’t as simple or elegant as you might expect. Encoding the precedence and associativity rules into a grammar that is unambiguous (and can be handled by LL and LR parsers) is pretty ugly and nonintuitive. This is one reason why LL and LR parsers are often extended with capabilities that let you specify operator precedence; for example, see the precedence features of Bison.”

• Human Calculator syntax
• Depends on order of operations

Postfix §

• AKA Reverse Polish Notation (RPN)

Conversions §

prefix to postfix §

• Can be done only w a stack

// PN to RPN
1. Split in to 3 iterator ranges: tokens 1, 2 and (3 to N)
    ( + )( 1 )(*  2  3)
2. Output token 2
3. If length of range(3 to N) > 1 recurse, else output token 3
4. Output token 1.

postfix to prefix §

• Can be done only w a stack

// RPN to PN
1. Split in to 3 iterator ranges: tokens 1, (2 to N-1) and N
   ( 1 ) ( 2 3 * ) ( + )
2. Output token N
3. Output token 1
4. If length of range(2 to N-1) > 1 recurse, else output token 2.

infix to postfix §

• Shunting Yard Algo by God

Subsets §

Deterministic Contest free languages §

• Un-ambiguous, can be processed in linear time

Left Recursion §

• Some rules (indirectly) reference themselves before any other (they are on the left of the rule). See left-recursive
  • Gets complicated if rule matches empty string

Examples §

See Left Recursion · PhilippeSigaud/Pegged Wiki · GitHub

• Direct: Caused by a rule referencing itself in the left-most position.

  A = A
  A = A | B | C | D | E | F ...

• Indirect

  A = B
  B = A
  =>
  A = A
  A = A
  =>
  A = A

Issues §

• A formal grammar that contains left recursion cannot be parsed by a LL(k)-parser or other naive recursive descent parser.
• In the example above, a top down parser would try parsing A and then again A and then again…, never gets to B
• The basic problem is that with a recursive descent parser, left-recursion causes instant death by stack overflow.
• Only a few things are naturally left-recursive, most left-recursion is a hack to get iteration, which LL parser generators have built-in.

Remove left recursion §

source: eli5 left recursion

A =
  | A x y z
  | B
  | C

# 1) Removing self-reference in leftmost position
A =
  |   x y z
    ^-- Yoink!
  | B
  | C

# 2) Find alternatives
A =
  | ... <- We're transforming this rule so we ignore it
  | B <- There's an alternative!
  | C <- There's an alternative!

# 3) Fill the leftover hole with all possible alternatives
A =
  | (B | C) x y z
    ^^^^^^^-- Plop!
  | B
  | C

# 4) Secret step: simplify (this is actually called left-factoring,
# not to be confused with factoring out left-recursion)
A =
  | (B | C) x y z
    ^^^^^^^-- Same pattern!
  | (B | C) <- Same pattern!

# So we get

A = (B | C) (x y z)?

To read §