Chomsky Hierarchy

tags : Regular Expressions, Automata Theory

The Chomsky hierarchy is descriptive. It simply allows us to broadly categorize grammars based on their capabilities.

The Hierarchy of Grammars (Generative Grammars) §

• The hierarchy allows us to broadly classify grammars based on their productive power.
• They have increasingly strict production rules and can therefore express fewer formal languages.
• Type 2 and Type 3 are popular

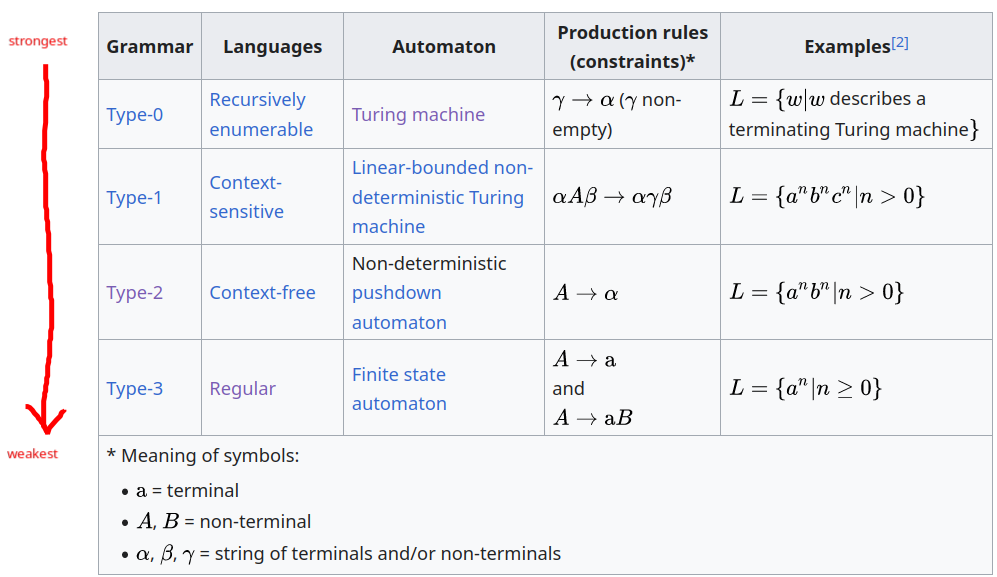
Type 0 (Recursively Enumerable) §

• AKA Unrestricted grammar

Type 1 (Context Sensitive) §

• all context-free languages are also context-sensitive languages, but some languages are neither context-sensitive nor context-free.
• context-sensitivity is often not resolved in the parsing phase but in later phases
• Writing context-sensitive grammars is very difficult for people to do without spending a lot of time and effort on it. The CFGs, though technically inaccurate, often give us enough to work with that they can be useful.
• Most languages are actually context sensitive

Type 2 (Context Free) §

• Used to parse programming languages
• The classic example people is x * y; in C, which is either multiplication or a variable declaration, depending on whether x is a type or a value. This proves that C cannot be a context-free language. i.e there exists context that’s not encoded in the text already.
  • Solution to this is Lexer hack , giving access to some kind of symbol table to the lexer
• CFGs are not nearly powerful enough to describe natural language because natural languages are ungainly and complex.
• X-bar theory is essentially the application of CFGs to language modeling

Type 3 (Regular Languages) §

• It’s not ideal to parse programming languages(Type 2) with regular expression hence.
• Things that Regular Expressions can parse (?)

Languages classes §

• Set of languages. Eg. The regular languages

Properties §

Decision Properties §

• Eg. Empty, Finite, Infinite?, Does the protocol terminate, Does the protocol fail?
• Harder to answer for larger classes of languages

Closure Properties §

• Given languages in the class, an operation (e.g., union) produces another language in the same class.

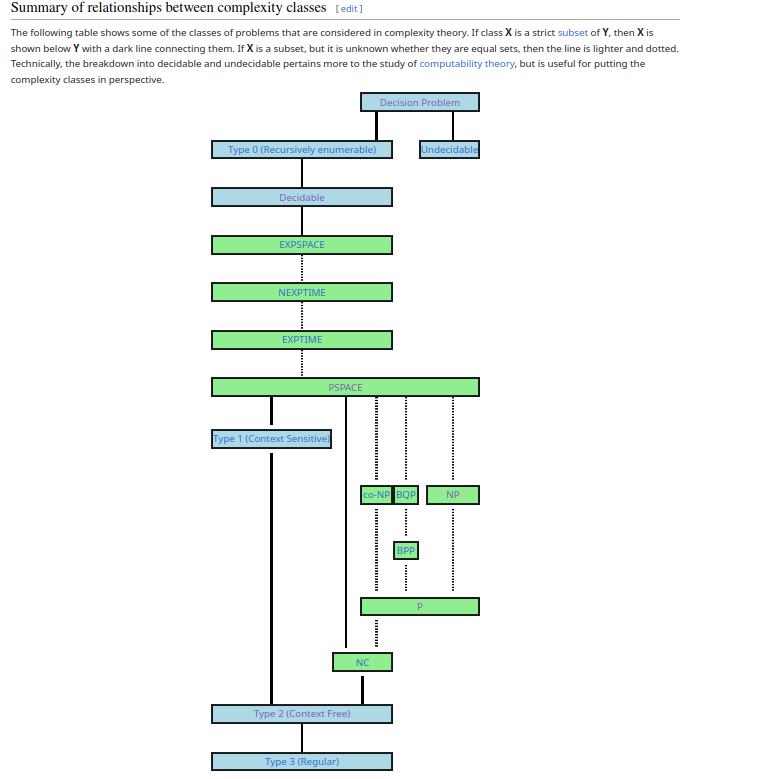
Regular Languages §

• A language that is accepted by a Finite Automata
• Proofs for decision properties for regular languages require RE or DFA.

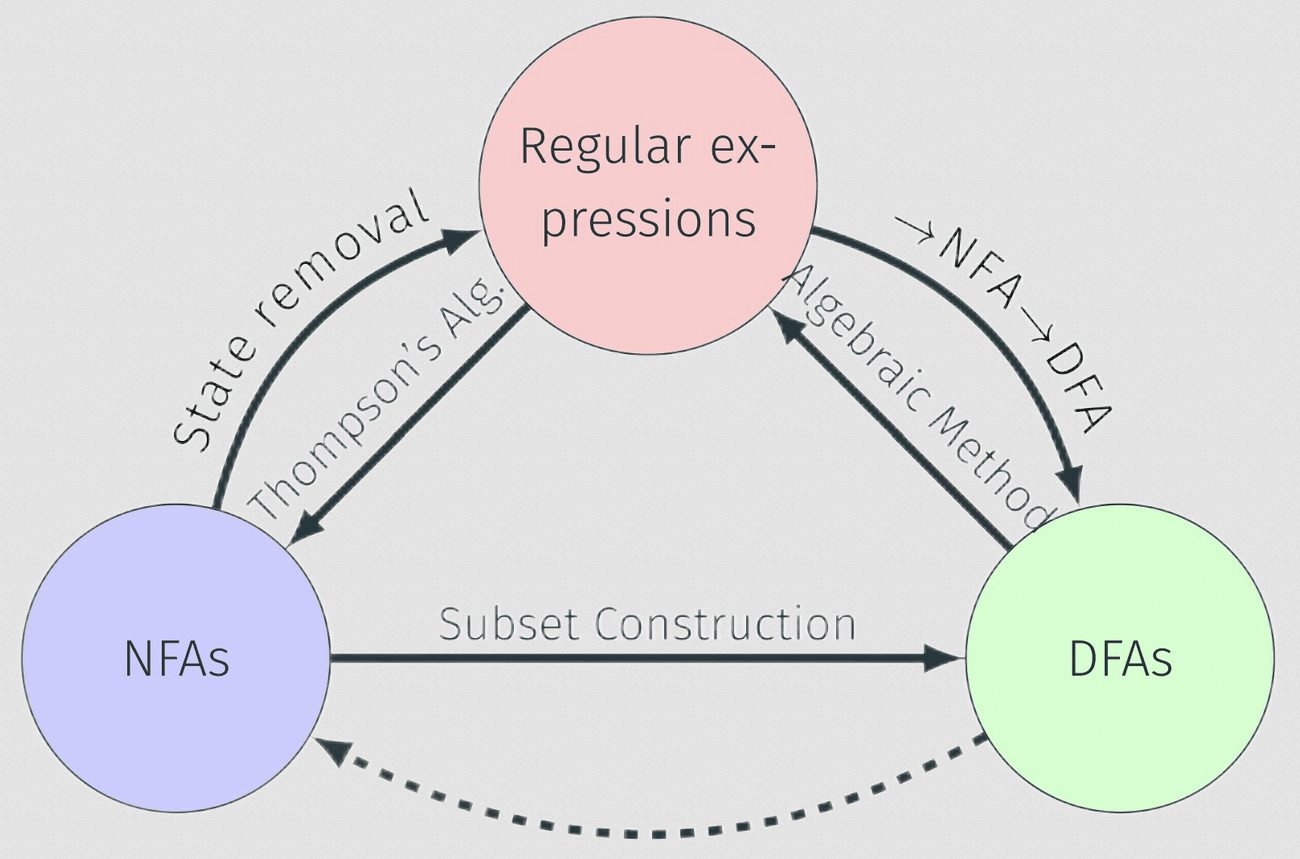
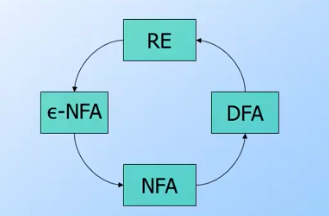
Descriptors §

• Regular Expressions
• FA/FSM/DFA/NDFA/NFA (See Finite Automata)

Context Free Languages §

• Let us do things that regular languages can’t do. Eg. Lets us process natural and programming languages, Match parenthesis or XML tags etc.
• Powerful than Regular Expressions and Finite Automata but still cannot define all possible languages.

Descriptors §

• Context-free grammars

  See Context Free Grammar (CFG)

  • Recursive system for generating strings

• Pushdown Automata

  See Pushdown Automata

  • Generalization of Finite Automata(FA)

Recursively Enumerable Languages §

• Turning machines : It can tell us what can be computed by computation and what cannot be.

Grammars to Alphabet §

Although there are an infinite number of different things that can be said, or written down in a particular language, it is still possible to process and understand all of them with a finite number of re-write rules. The name given to a set of re-write rules is a grammar

• Grammars are defined by Languages
• Languages are defined by set of Strings
• Strings are defined by sequence of Symbols
• Set of Symbols is defined by the Alphabet

Grammar §

• Whenever we put restriction on a language, we create a grammar

Language §

• A set of strings accepted by an automaton A is the language for A
• Eg. If A accepts s-o and s-o-o, then set of these 2 strings represent the language for A
• Denoted by L(A)
• Different types of Automatons accept different languages
• They can be finite or infinite sets
• Personal Note: L(Alphabet) , L(Automaton) seem like the same thing.

String §

• Eg. In C, "O" is string, while '0' is a character/symbol.

Alphabet §

• Finite set of symbols
• Eg. ASCII, Unicode, {0,1}, {a,b,c}, set of signals used by some communication protocol

Resources §

• Good summary: https://www.reddit.com/r/compsci/comments/aqdlpy/what_are_some_real_applications_of_the_chomsky/eggu89g/