Finite Automata

tags : Automata Theory, Regular Expressions, Chomsky Hierarchy

Intro §

• A formal system
• Remembers only a finite amount of information. Intuitively, they cannot count beyond a fixed number.
• aka
  • finite-state machine (FSM)
  • finite-state automaton (FSA)
  • finite automaton (FA)
  • state machine
• Characteristics
  • state: Information representation
  • inputs: states respond to inputs
  • transition: Rules that tell how to change in response.

Regular Languages §

• All finite languages are regular
• Some infinite languages are regular

Non-regular languages example §

• FA system cannot handle non-regular languages.
• To handle these, we need more powerful systems like Push down Automata or CFG.
• There are ways to prove a non-regular language, eg. Pumping Lemma

Regular language example §

• Eg. the strings that represent floating point numbers in your favorite language is a regular language.

NFA and DFA §

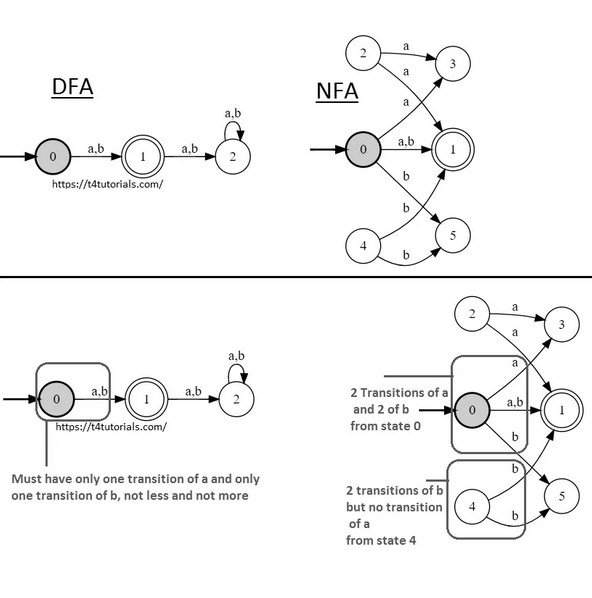
DFA §

• Every DFA is an NFA, but opp. not true
• Exactly one sequence of steps for each string

NFA/NDFA §

• May have many sequences of steps for each string

ε-NFA §

• Each has its own final state.
• NFA that allows null/empty moves