Data Structures

tags : Algorithms, Bit Shifting

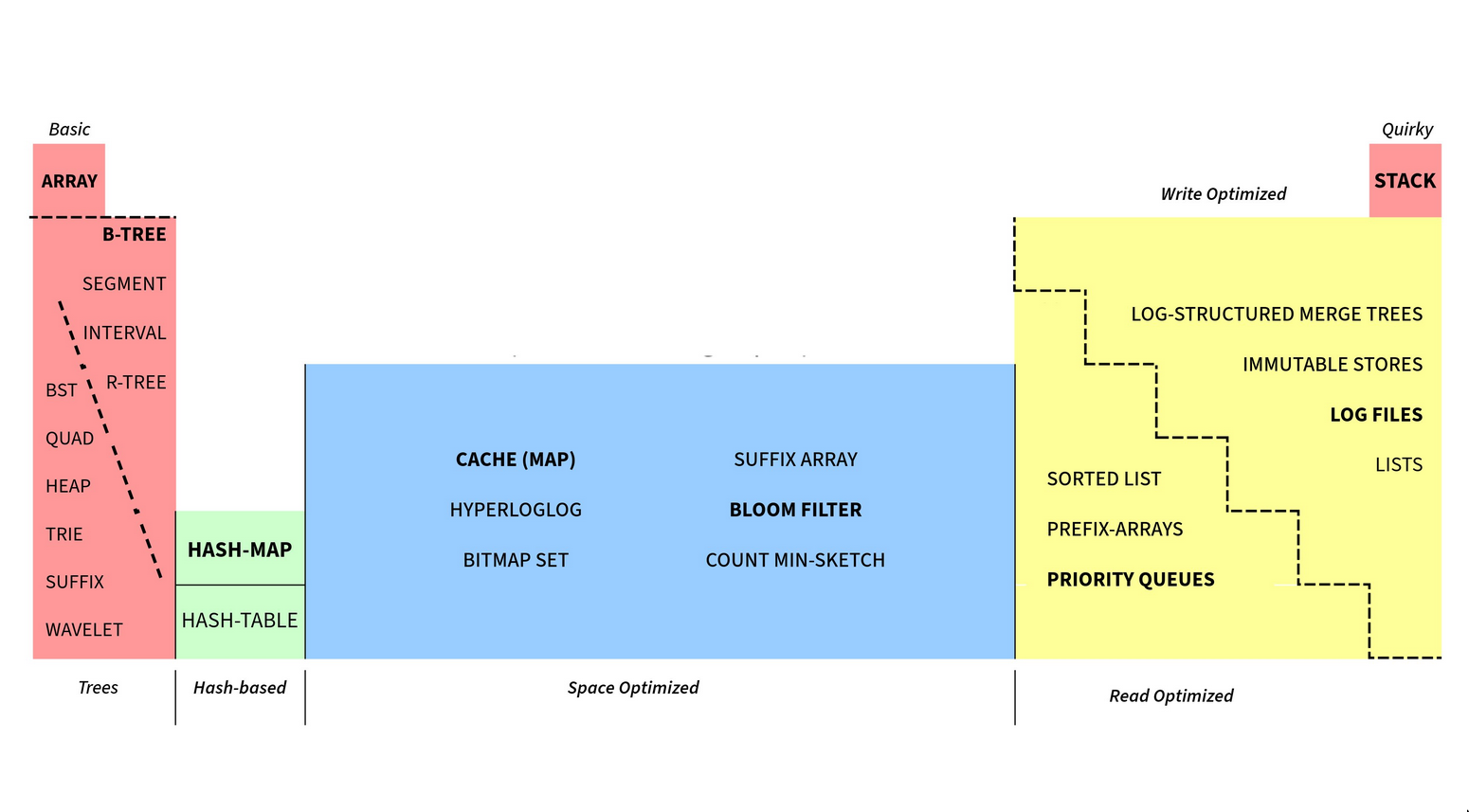image found on twitter^ (gkcs_)

Abstract data types §

• When we start questioning “is this a datastructure or an algorithm?”
• These are defined by what you can do with it; what operations it supports.
• Well, it uses a Data Structure and uses an Algorithm on top of the data structure.

Maps §

Hashmap/Hashtable §

See Hashing

Requirement §

• Stability: Given the same key, your hash function must return the same answer.
• Distribution: Given two near identical keys, the result should be wildly different.
• Load factor: Once the number of entries across each bucket passes some percentage of their total size(load factor)
  • The map will grow by doubling the number of buckets
  • Redistributing the entries across them.

Implementation §

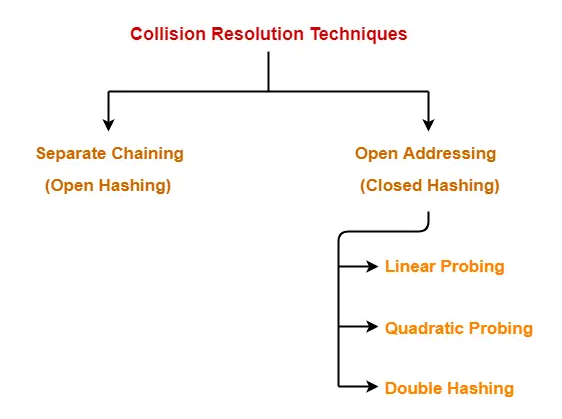
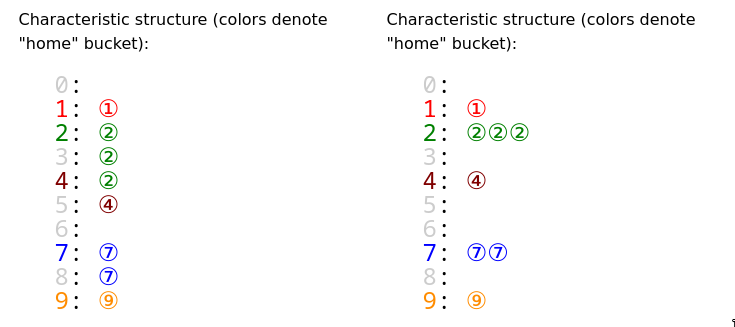
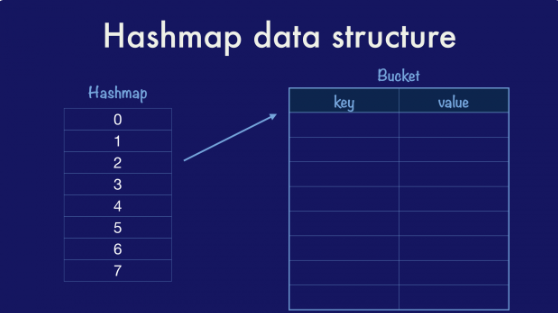
• Out of these two, online references to hash tables probably usually refer to “chain based”/“closed addressing” hash tables, where the address of the value is determined by the hash value.
• There’s nothing called “Closed Addressing” really. If it were, it’d mean chaining based only.
• The “hash table” is just the array+auxiliary store. Open and Closed Hashing determine whether there exists in auxiliary store.

Name	Other names	Description
Open Addressing	Closed Hashing	Location (“address”) of the element is not determined by its hash value. instead index may vary depending on what’s already in the hash table.
Closed Addressing	Open Hashing, simply Chaining, Separate Chaining	Each bucket is independent, and has some sort of ADT (list, binary search trees, etc) of entries with the same index.

Properties	Open Hashing / Chaining/Separate Chaining	Open Addressing/Closed Hashing
Address	- actual address in a “bucket”(some ADT) attached to the hash table array	- address/index of the element is not determined by its hash value
	- data is stored in a seperate structure, we call it seperate chaining	- index may vary depending on what’s already in the hash table
		- So we’re open about where how it gets “addressed”, the hash value doesn’t become a defining factor
Physical Location	- none of the objects are actually stored in the hash table’s array	- we never leave the hash table; every object is stored directly at an index in the hash table’s internal array.
	- all data is "open"/freed from the internal hash table array	- all data is closed in the hash table array (No buckets, only collisions)
Collision	- each cell in the array points to a ADT contain the "collisions"/"bucket"	- We store the collisions in the same array. Then we jump from collision to collision until we find the key.
Keys	- Arbitrary number of keys per bucket/collision	- At most one key per bucket/collision
Load factor	max 1	no max
Operation	Hash(Key) = Hashed_Key => mask(h_k) => bottom_bits(m_h_k) => bucket offset => key search	Hash(key) => initial position, if collision, use probing sequence to find the next available slot
Example	linked lists(not cache friendly), trees, sorted arrays etc.	Linear/Quad Probing, Double hashing,Cuckoo hashing etc

Worst case §

• WC can be caused by bad distribution/collision. Eg. All key resolutions point to the same bucket, now for the specific bucket it’ll be linear search so if everything gets dumped into the same bucket, you essentially have a linked list, i.e $O(n)$ running time for lookup.

Resources §

• Faster hash table probing
• Hash Tables
• https://twitter.com/FilasienoF/status/1717419319640883225

Merklizing the key/value store (merkle tree) §

See Trees

Bloom filters §

A fast index to tell if a value is probably in a table or certainly isn’t.

Maps ADTs 👀 §

LRU §

• Usually used for caching. It’s not exactly a FIFO because we update the position of things based on when they are accessed.
• We need fast lookup: Hashmap
• Once a value is fetched from the cache, we need to move the fetched value to the front of the list. So the end of the list will have the lru value.
• It’s like a combination of hashmap + linked list. The value points to actual nodes directly. Therefore we get $O(1)$ for
  • lookup/get : moving from position to front and return value
  • update
    • insertion-at-front (if new key)
    • moving from position to front (if updating existing key)
    • Even though update technically doesn’t mean they fetched the value, but they touched it. Our logic says, if its touched it’s used.
  • expand_cache: deletion-at-end (remove lru)

• Implementation

  

  • Eviction
    • When over capacity, we need to evict things.
    • Since eviction happens without user input. We need a way to know what key we have for our value. For this we need a reverseLookup map, then we can also delete the original key from the lookup map.

Lists §

Array §

• Pedantic definition here
• capacity must defined & allocated before using, otherwise cannot form array
• Cannot expand
• Good for random access

Linked list §

Technically, every linked list is a tree, which means every linked list is a graph.

• Node based data structure
• Singly linked, Doubly linked
• Better control over memory than array, you could create a object pool etc.
• You can’t do a binary search on a linked list, you must traverse. (I mean you can do but it’ll not be efficient for obvious reasons). So usually bad choice if you need random access.

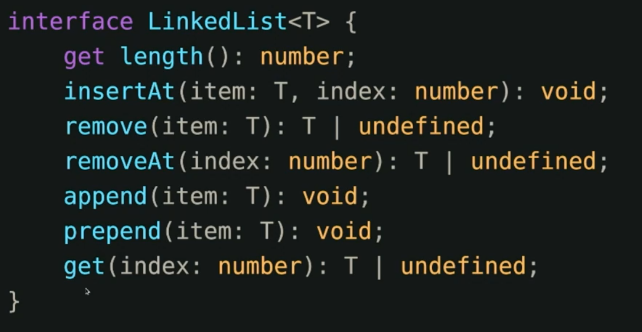
Linked List BAD for modern CPUs! §

From a reddit post:

When linked lists were first discussed in algorithms books in the 1970’s, processor speeds were roughly comparable to the speed of accessing main memory. So there wasn’t a substantial difference in cost between accessing the next element of an array vs the cost of following a pointer to the next element in a linked list.

But on modern computers the difference is staggering: the cpu can execute hundreds or even thousands of instructions in the time it takes to access a random address in memory. (And accessing the disk is thousands of times slower than that.)

To make up for this difference, for decades processors have been using caches: the L1 cache is built into the processor and is extremely fast but relatively small, the L2 cache is larger and slightly slower to access, the L3 cache is even larger and even slower.

The caches do a lot to mitigate the cost of accessing memory, but they work best when you’re accessing contiguous blocks of memory.

And that’s why linked lists don’t do as well in practice as they seem to when you just count the number of instructions they execute.

With a linked list, every time you traverse to the next item in the list, you’re jumping to a totally random location in memory, and there’s a decent chance that address isn’t in cache.

With an array, getting the next element in the array is in adjacent memory, so after the first access the rest of the array is probably cached.

So, what most people find is that in practice, a dynamic array is much faster in practice for many common list sizes.

Also, keep in mind that linked lists are not necessarily that efficient in terms of memory: if each item is 8 bytes or smaller, then every item in the list needs an additional 8 bytes of overhead (for the pointer). So a linked list might have 2x overhead, while a dynamically growing array might perform quite well with only 25% overhead.

Of course, it totally depends on the exact usage. There are absolutely cases where linked lists perform better than alternatives, and they should still be used in those cases.

• c++ - Bjarne Stroustrup says we must avoid linked lists - Stack Overflow
• In defense of linked lists | Hacker News

Dynamic Array/Array List §

• Rapper names: grow-able array, array list
• Implementations: Go Slices, Java ArrayList, Python’s list, Javascript []
• You get: Random access. Well suited for stack likes (LIFO)
• insert/remove at the end/tail is $O(1)$, good stuff
• insert/remove at the start/head is $O(n)$, pretty bad
• Optimal stack implementation is possible, Optimal queue implementation is not possible.
  • i.e Implementing a queue in Javascript with .push and .shift is probably not the best idea. But there have been improvements in .shift recently.
• Whenever there is no room for appending a new element
  • It creates a larger array
  • Copies the contents of the current array to it
  • Deletes the current array
  • Sets the newly created array as current
  • Finally, appends the element normally.

Array Buffer / Ring Buffer / Circular buffer §

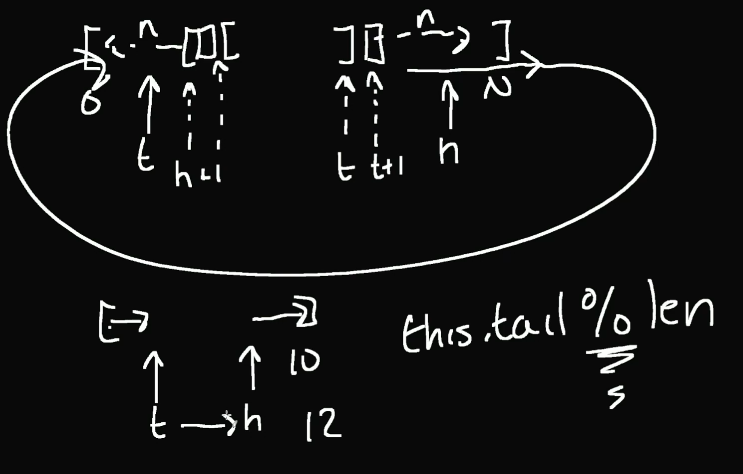
• No fixed head or tail. This also grows like Dynamic arrays but at the same time maintains order.
• No shifting of other elements in the buffer needed at insertion/removal unlike dynamic array/arraylist. So, Well suited for queue like interfaces (FIFO)
• You can implement things like queue/double ended queue(deque)/circular queue etc. w it.
• Circular Buffer Performance Trick - Cybernetist

List ADTs 👀 §

Queue §

• Can be implemented on top of a Linked List data structure.
  • It constrains what you can do with a linked list.
  • We don’t even need a doubly linked list to implement a basic queue.
• FIFO
  • The algorithm a queue implements is FIFO.
  • FIFO is bad for temporal locality
• Interface
  • insert-at-end : $O(1)$ (aka enqueue)
  • remove-at-front : $O(1)$ (aka dequeue)

Stack §

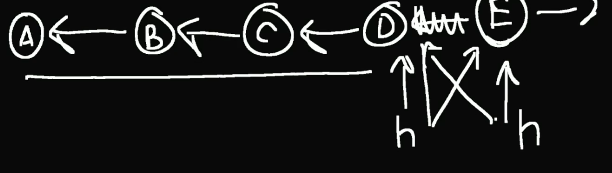
• LIFO
  • LIFO is good for temporal locality
• Good to think of arrows pointing backwards from the head. So usually just prev on a Node works.
• Interface
  • insert-at-end : $O(1)$ (aka push)
  • remove-at-end : $O(1)$ (aka pop)

Deque (double ended queue) §

• Not to be confused w the dequeue operation. (Spelling is different! ue)
• This is an abstract data type, Java has an implementation of this interface. It can be implemented via Linked list/or some custom implementation like Java does with ArrayDeque.
• insert-at-end : $O(1)$ (aka enqueue / push)
• remove-at-end : $O(1)$ (aka pop)
• remove-at-front : $O(1)$ (aka dequeue)
• insert-at-front : $O(1)$

In Java, ArrayDeque doesn’t have

• The overhead of node allocations that LinkedList does
• The overhead of shifting the array contents left on remove that ArrayList has.
• So eg. in Java, if you had to implement a Queue, you’d go with ArrayDeque as the underlying data structure rather than LinkedList or ArrayList.
• Summary: It’s pretty good.

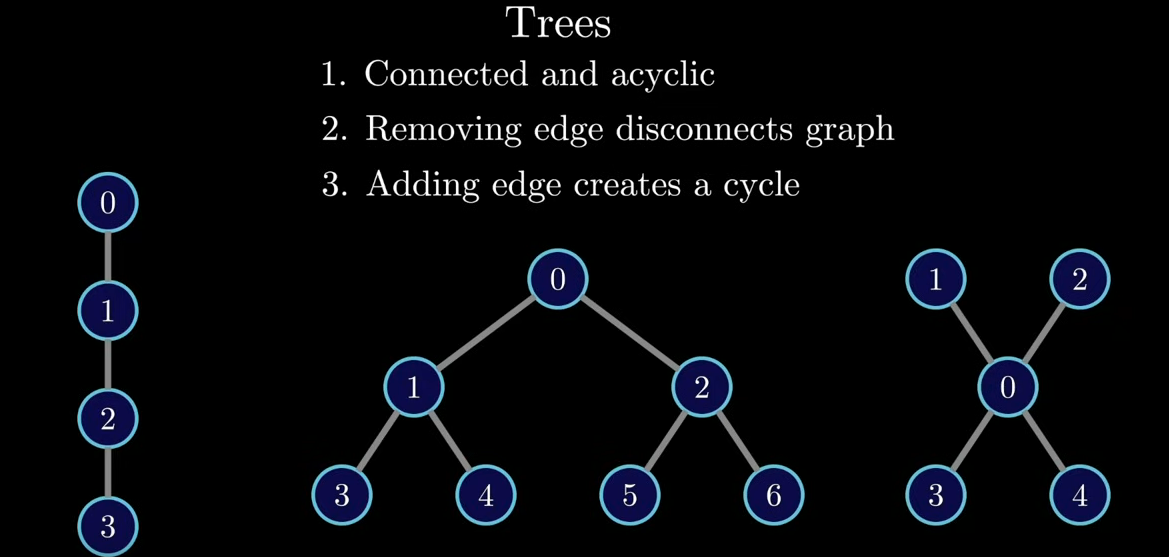
Trees §

• Technically, trees are just linked-lists with multiple paths.
• Trees are also graphs
• i.e link list = tree = graph

See Trees

Tree ADTs 👀 §

• Priority Queue (Implemented using Heap)

Graphs §

• See Graphs