tags : Complexity Theory, Math
What is it?
- A language to talk about functions
- We’re just talking about properties of functions
- We’re not talking about meanings
- Programmers use this notation to describe complexity, but there’s absolutely nothing stopping us from using asymptotic notation with other types of equations, things like the population of rabbits over time, the temperature given a change in pressure, and so forth.
The notation
-
- actually means
- read as ” is order ” or ” is ”
The Details
-
Functions are sometimes complex (Wiggly curve in diagram), so it’s easier to talk about the function in terms of upper bound and lower bound.
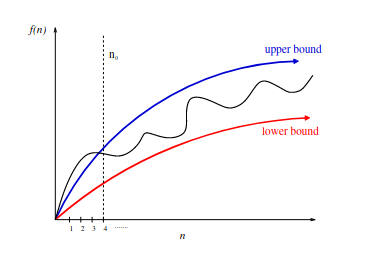
-
What are the bounds?
- Upper bounded = (best known upper bound, or a simplification of the best-known upper bound, actually care about in practice)
- Lower bounded = (notoriously difficult to prove)
- Theta bounded =
-
With Big Oh Notation, we are able to reason about complex functions because we can see the upper and lower bound of the function.
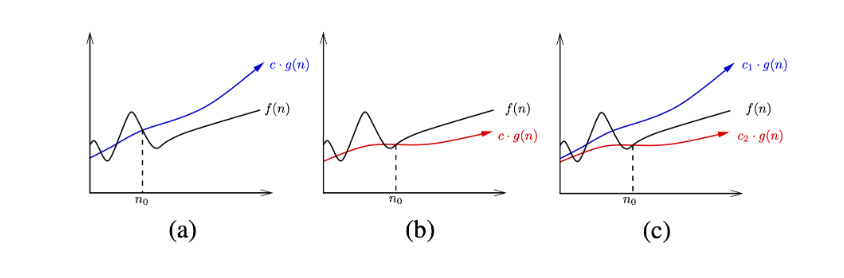
- means is upper bound on
- means is lower bound on
- means
- is upper bound on
- and is lower bound on
- relationships for a function will be satisfied for and .
- is
constantindependent of - is a
constant, a threshold beyond which these are satisfied - We do not care about small values of
- is