Statistics

tags : Math, Causal Inference,

![](/ox-hugo/20231017200424-statistics-830473767.png)

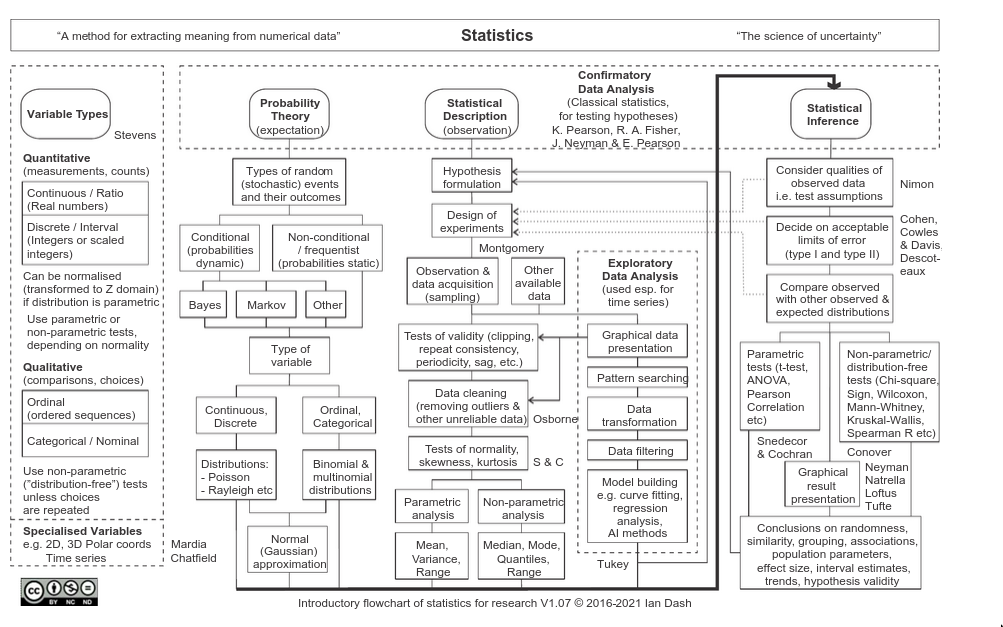
Stats is about changing your mind under uncertainty

FAQ §

Bayesian or Frequentist §

• The difference is philosophical
• The statistical war is over, we no longer talk about this
• We’re more interested in how we justify our statistical procedures, whether they’re Bayesian or frequentist, which leads us to Causal Inference
  • The right one to choose depends on how you want to approach your decision-making.
  • Eg. If you have no default action, go Bayesian.
• Also see Bayesian Statistics: The three cultures | Hacker News

Differences §

	Bayesian	Frequentist
Parameter	It is a random variable. It’s perspective, no right or wrong.	It’s not a random variable. Answer is fixed and unknown, there’s one “right answer”
Goal	Opinions to have (prior belief)	Actions to take (default action)
Thinking	I have an perspective, let’s see how it changes if i add data to it	We try to figure out an evidence that convinces me to choose an action
Coin-Toss	It’s 50% heads for me, but 100% for you because you know already	It’s 100% either heads or tails, I just don’t know the answer
Jargon	credible interval, prior, posterior	confidence interval, p-value, power, significance, method quality

Difference between statistics and analytics §

• Analytics
  • We always learn something (scope of your interest is the data that’s in front)
  • Analytics cares about what’s here. i.e Stick to the data and don’t go beyond it.
  • When you go beyond your data, you venture into statistics
• Statics
  • Sometimes we do something with the sample and it tells us nothing about the population
  • It’s okay and good to learn nothing in statistics after analyzing our data/testing your hypothesis.
  • Statistics cares more about what isn’t.

Rounding Numbers §

It was surprising to me that I am was on the wrong side when coming to rounding numbers! Most important thing is to round in one step and to round in the last step of the calculation.

• Draw a line mentally at the point where you want to round.
• If the number next to the line is 0-4, throw away everything to the right of the line.
• If the number next to the line is 5-9, raise the digit to the left by one and throw away everything to the right of the line.

Eg. 1.2|4768 ~ 1.2 but 1.2|7432 ~ 1.3

Basics §

Sample and Population §

Because of this, we can see two versions of formulas, one for population and one for sample

Population §

There are no set rules to apply when defining a population except knowledge, common sense, and judgment

Sample §

• It’s an approximation of the population
• Always will have some error in them
• It is usually a subgroup of the population, but in a census, the whole population is the sample. The sample size is usually denoted as n and the population size as N and the sample size is always a definite number.

• Good and bad samples

  A good sample is a smaller group that is representative of the population, all valid samples are chosen through probability means. Following are some ways to collect samples, ordered by preference:

  • Random Samples

    Random doesn’t mean unplanned; even collecting random samples needs proper planning. For this, you need a list and some way to select random subjects from the list for your sample.

  • Systematic Samples

    Best explained through an example, Standing outside the grocery store all day, you survey every 40th person. That is a systematic sample with k=40.

  • Cluster Samples

    This one makes a big assumption, that the individuals in each cluster are representative of the whole population. A cluster sample cannot be analyzed in all the same ways as random or systematic samples. You subdivide the population into a large number of subunits(clusters) and then construct random samples from the clusters.

  • Stratified Samples

    This needs analyzing what data you’ll be working with, if you can identify subgroups(strata) that have something in common related to what you’re trying to study, you want to ensure that you have the same mix of those groups as the population. Eg. 45% Girls and 55% Boys in a school, If you’re taking samples of 400, it should be 45% x 400 and 55% x 400, each mini sample should be constructed using other random sampling methods.

  • Census

    A census sample contains every member of the population.

Statistics types §

Descriptive Statistics §

• Summarizing and presenting the data that was measured
• Can be done for both quantitative and categorical data
• statistic
  • a statement of Descriptive stats
  • a numerical summary of a sample

Inferential Statistics §

• Making statements about the population based on measurements of a smaller sample.
• INFERENCE = DATA + ASSUMPTIONS, i.e statistics does not give you truth. The way to “require less data” is to make bigger assumptions.
• An assumption is not a fact, it’s some nonsense you make up precisely because you’ve got gaping holes in your knowledge. But they’re important.
• parameter
  • a statement of Inferential stats
  • a numerical summary of a population

Errors §

In stats, errors are not like programing errors but are the discrepancy between your findings and reality.

Sampling error §

These are part of the sampling process, cannot be eliminated can be minimized by increasing the sample size

Non-sampling error §

When you mess up in collecting data/analyzing data etc.

Data and experiments §

Variables §

Variables are the question and data points are the answers. Eg. birth weight is the variable and 5Kg will be the data point. sometimes variable type is also called data type.

In either observational study or experimental study there are two variables:

• Explanatory variables/factors: Suspected causes
• Response variables: Suspected effects/results

• Explanatory variables that make the results/response variables questionable:

  • Lurking variables: A hidden variable that isn’t measured but affects the outcome. A careful randomized experimental study can get rid of these.

  • Confounding variables: You know what they are, but you cannot untangle their effect from what you actually wanted. Try to rule these out if possible before experimentation.

• Quantitative and Qualitative

  • Quantitative

    Numeric, sometimes it’s hard to differentiate between discrete and contd. but it’s important to identify the difference when you need to graph them

    • Discrete: how many
    • Contd. : how much

  • Qualitative/Categorical

    non-numeric

Gathering data §

• Observational study

  A retrospective study. Lurking variables are the reason an obs study can never establish cause/causation, no matter how strong of an association do you find.

• Experiment

  Here we can manipulate the explanatory variables, each level of the assigned explanatory variable is known as a treatment. If we do have a randomized experiment, we can prove causation. Eg. Doing a study by giving your 3 children different toys, the explanatory variable is toy, and treatments are the different toys.

Basics of designing experiments §

Completely Randomized Design §

Randomly assign members to the various treatment groups, this is called randomization

Randomized Block Design §

When there is a confounding variable that you can detect, before conducting the experiment divide subjects into blocks according to that variable, then randomize within each block. This variable is called the blocking variable. i.e confounding variable became the blocking variable here.

“Block what you can, randomize what you cannot”

Matched pairs §

Type of randomized block design where each block contains two identical subjects without any fear of lurking variables. (Eg. twins) another special type is matching experimental results with itself (eg. delta)

Control groups and placebo §

When doing experiments involving the placebo effect, the group that gets the placebo is called the control group

Distributions §

Meta §

• Distributions themselves are not specific to either frequentist or Bayesian statistics
• Frequentist statistics uses distributions to model the frequency of data and outcomes.
• Bayesian statistics uses distributions to model the probability and uncertainty of parameters.

Frequency Distribution §

Descriptive Stats §

3M (Center of Data) §

• Mean, Median and Mode
• Measure the center of the data

Mean §

• Arithmetic Mean/Sample mean

  • Useful for additive processes

• Geometric Mean

  • Useful for multiplicative processes
  • Useful w Growth rates because they depend on multiplication and not in addition

Median §

• sort data in inc order
• odd observations: middle value of data array
• even observations: mean of the 2 middle values of data array

Mode §

• Observation that occurs the most
• Dataset can have one, multiple or no modes

Median vs Mean §

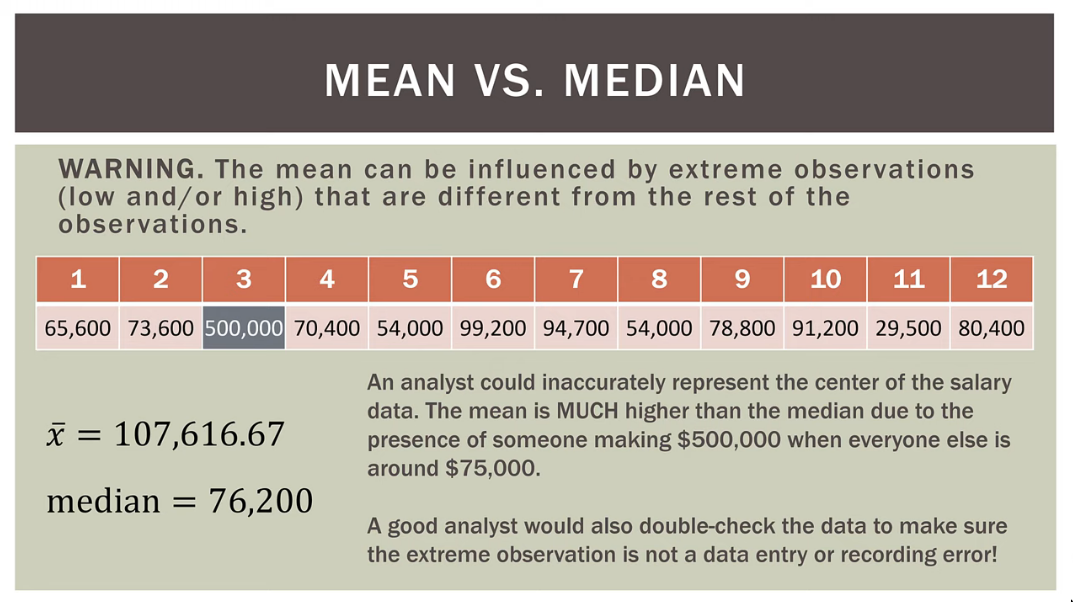Solution can be Trimmed Mean

Percentiles, Quartiles(4), Quintiles(5), & Deciles(10) §

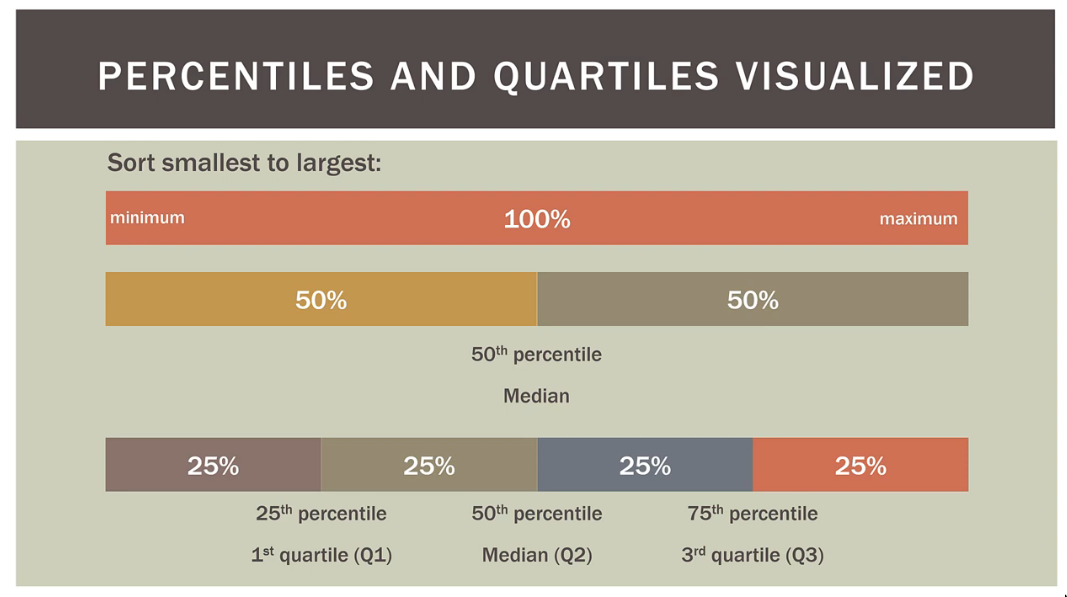
• These just help us locate an observation in a sorted (low to max) dataset; an address
  • Doesn’t have to a value in the dataset.
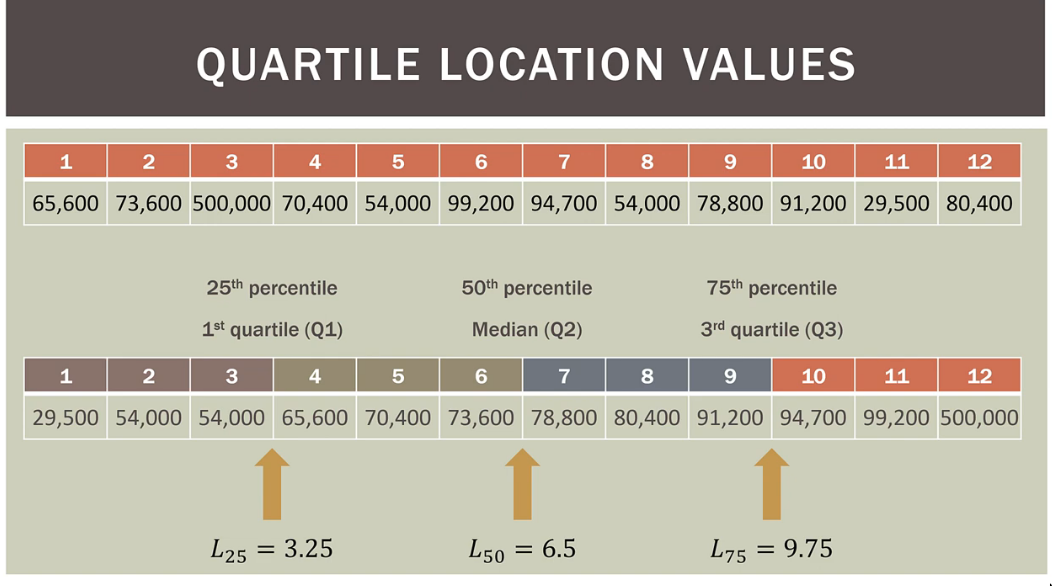
  • There’s a location formula, we can calculate the actual value of the percentile from the location even if the address doesn’t point to a data point
• Quartiles, Quintiles, & Deciles are variants of percetile
• Percentiles
  • The number of values out of the total that are at or below that percentile
  • The observations lie below the said percentile or above the said percentile
• Formula to find percentile for some data point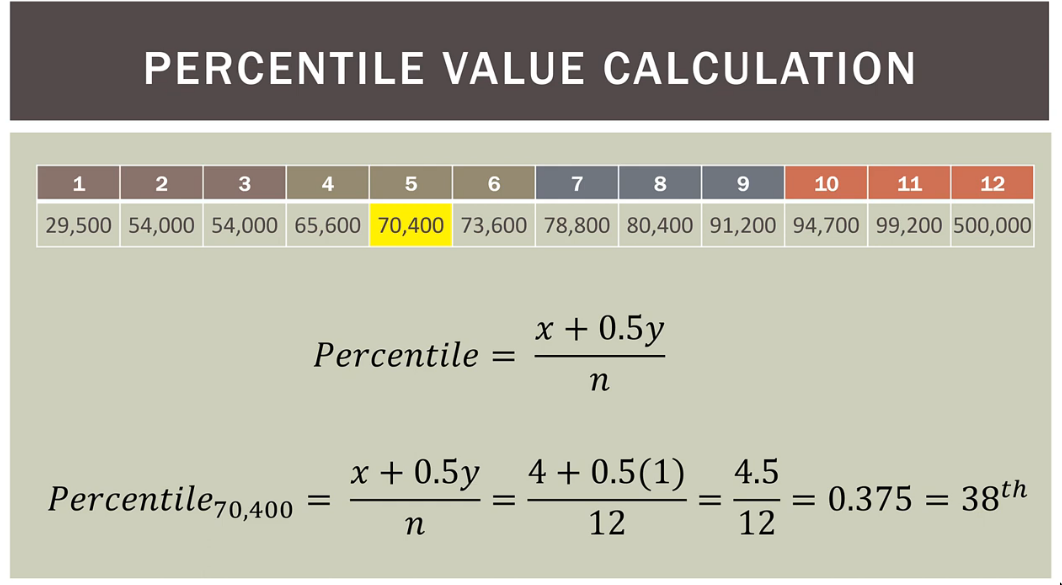

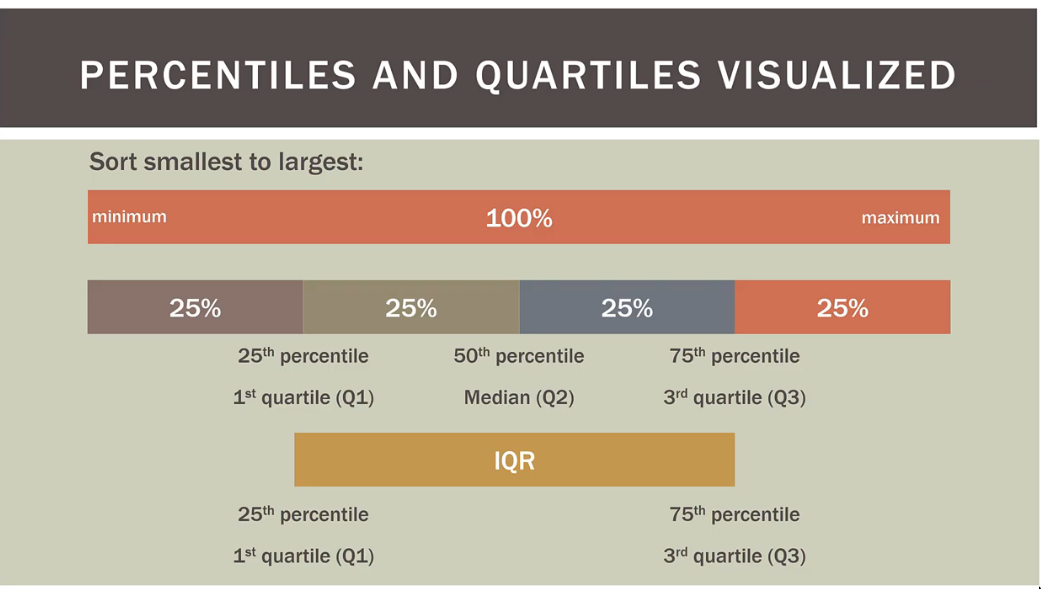
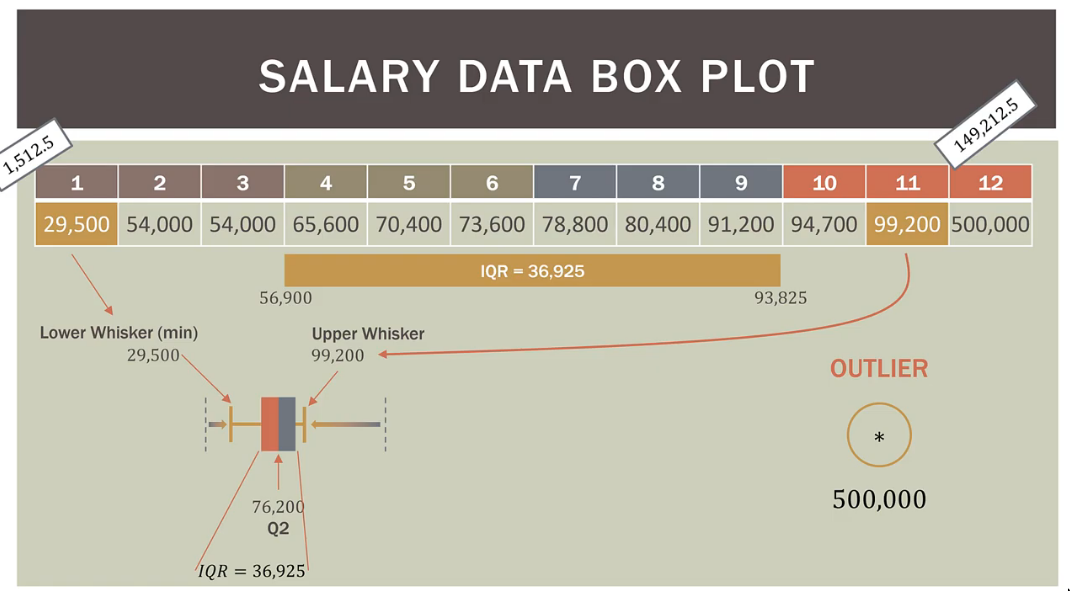
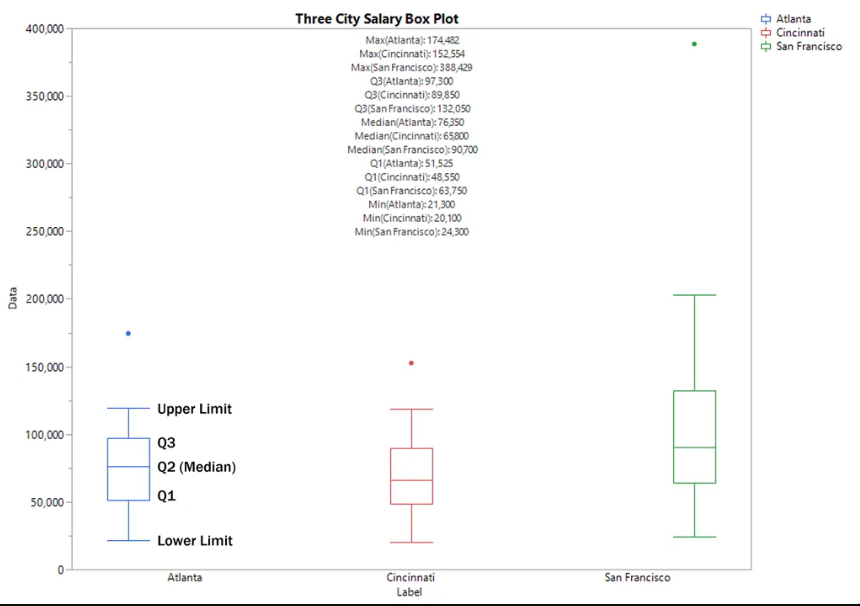
IQR (Inter Quartile(4) Range) §

The median will lie somewhere in between the IQR

Variability §

• Useful when comparing datasets
• Related to the mean
• If things are “spread out”
• Variability answers, “How far is each data point from the mean? (DISTANCE)”

Standard Deviation §

• Standard Deviation is just the positive square root of the variance
  • SD is the sqrt of the sum of the square of the difference of the data point and the mean divided by the no. of observations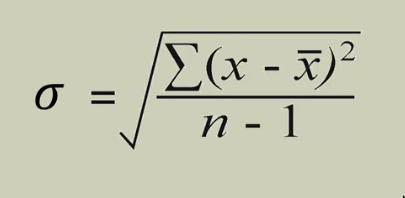
  • SD has the convenience of being expressed in units of the original variable. Which is not the case with variance.
• What it says?
  • If most data points are close to the mean, variance & SD will be lower
  • If most data points are further to the mean(spread out), variance & SD will be higher

Z-score §

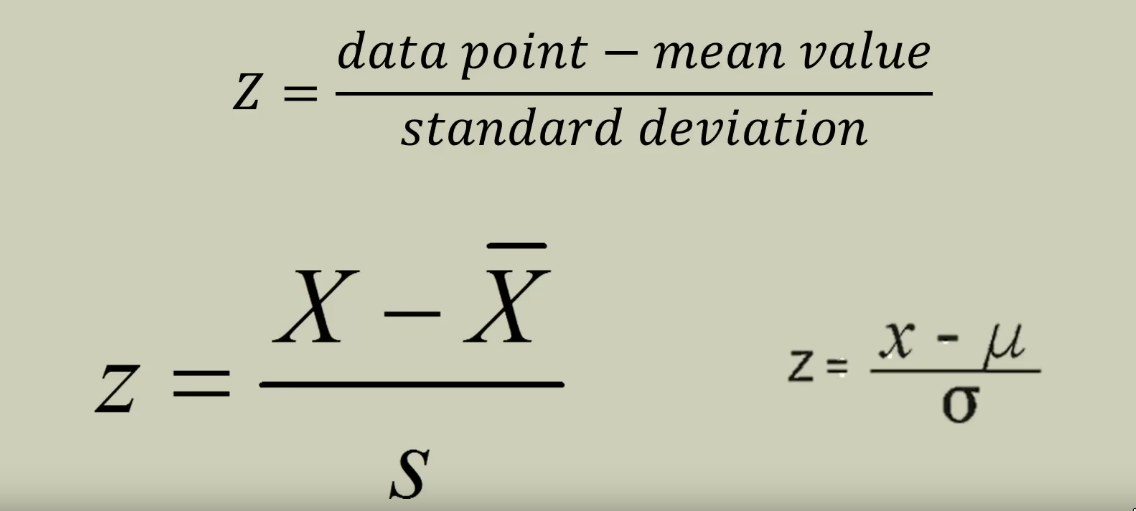
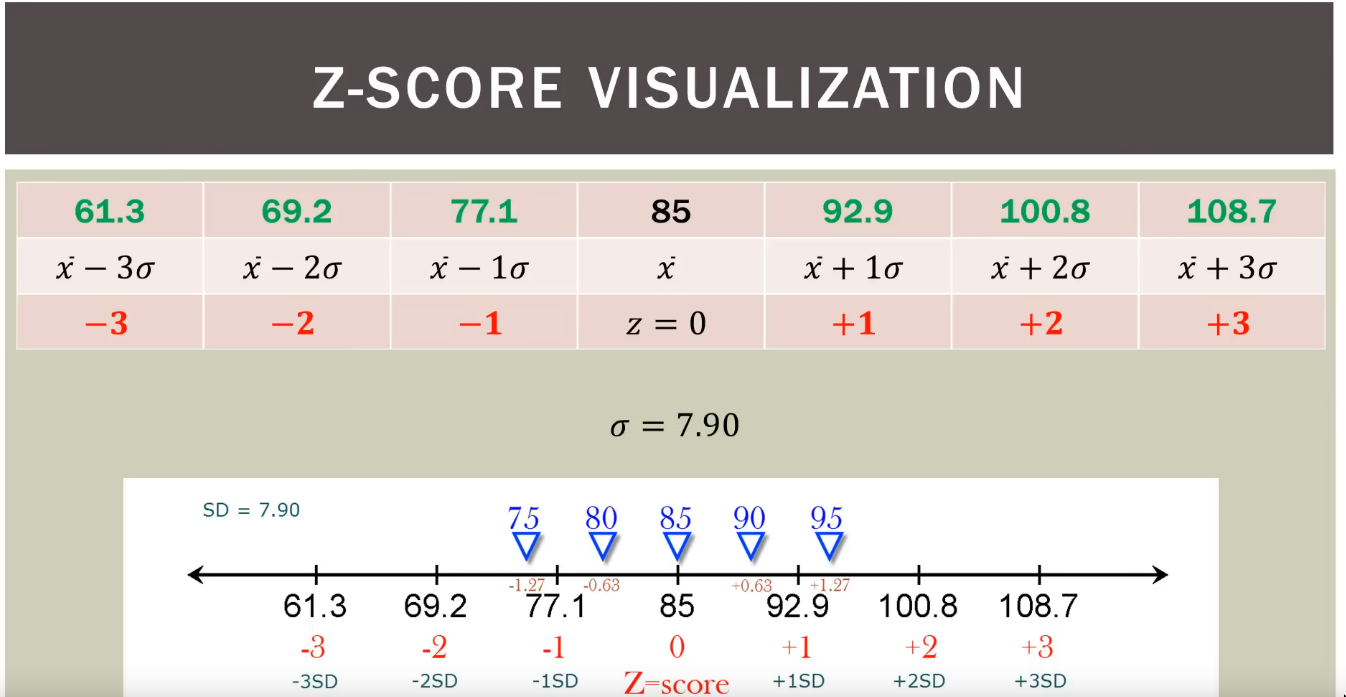
• Z-score answers: “How far is any given data point from the mean? (DISTANCE)”
  • How many SD away from the mean? (It measures distance in the unit of sd and ignores any original units such as inches/hours etc.)
• The Z-score for the mean itself is 0 because, it’s 0 distance away from the mean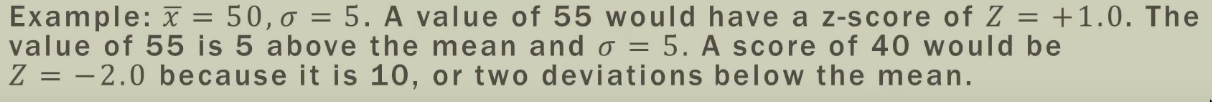

Bi-variance §

Relationship between two variables

• Covariance

  

  • Shows the linear association btwn 2 variables.
  • It shows the direction, not the strength
    • +ve: increasing linear relation
    • -ve: decreasing linear relation
  • No upper/lower bounds, scale depends on variables
  • Covariance Matrix

• Correlation

  

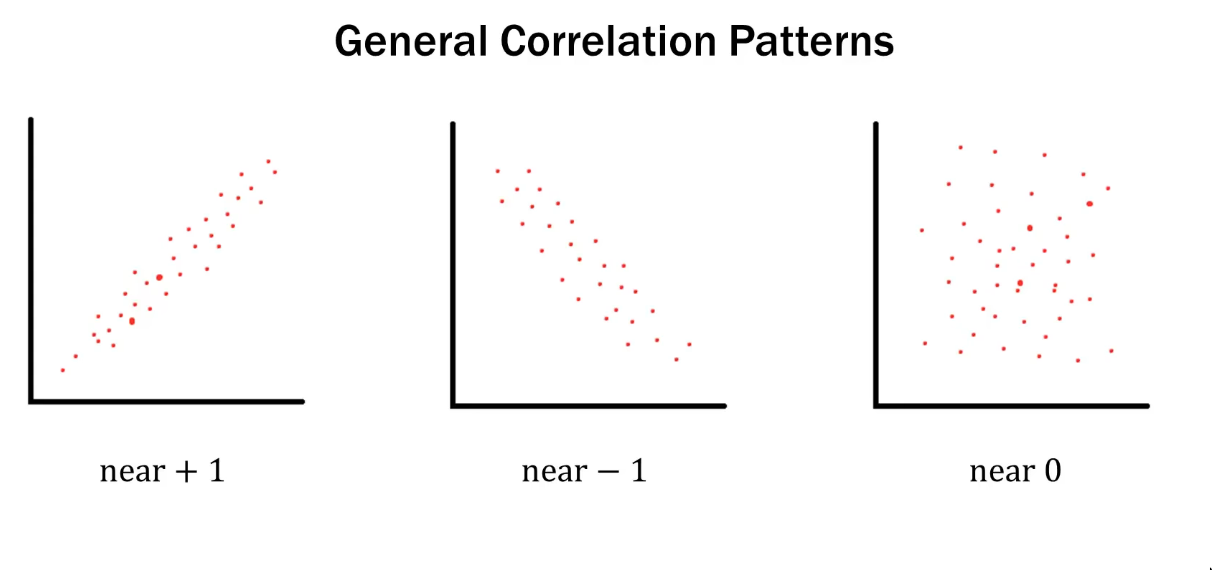
  • It shows the direction, AND the strength
    • strength of correlation does not mean the correlation is statically significant
  • Only applicable to linear relations
  • Always between -1 and 1, i.e scale is independent of the scale of the variables
  • Covariance is not standarized, correlation is standarized. i.e we can use correlation to compare two data sets using different units etc.

• Linear Regression

• Non Linear data

  

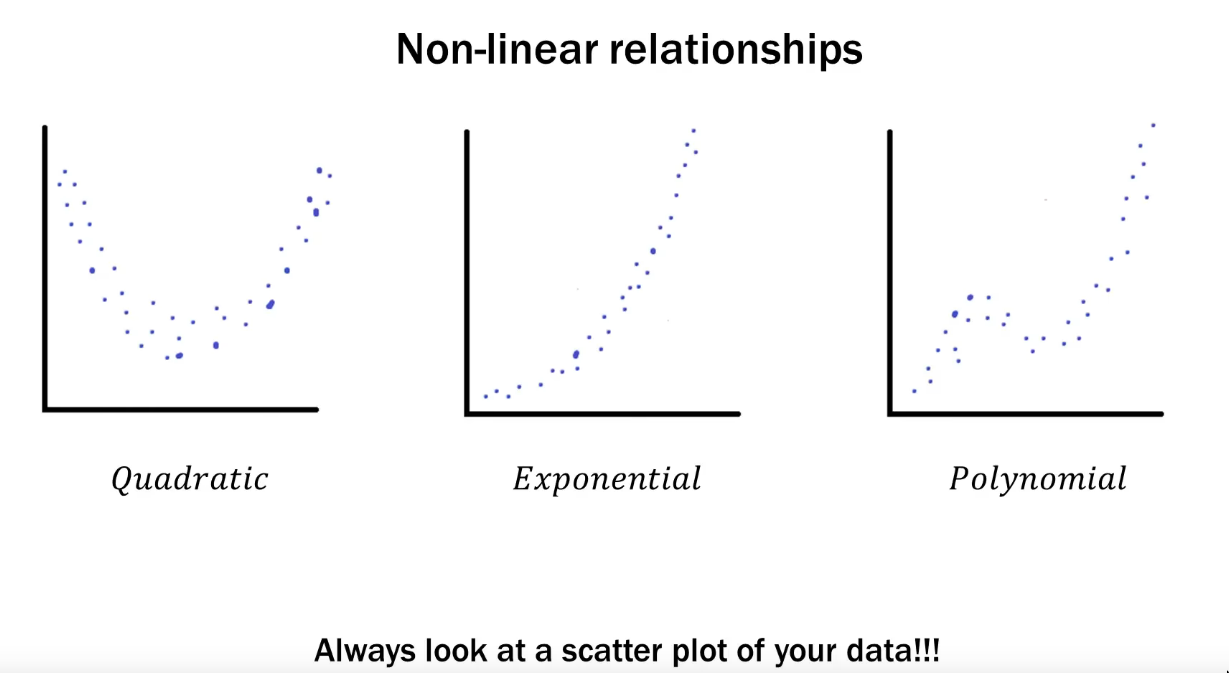
Hypothesis testing §

Bayesian approach §

Process §

• Unlike frequentist approach, result is not an action but credible intervals
• credible intervals: 2 numbers which are interpreted as, “I believe the answer lives between here and here”

TODO Null Models? §

Frequentist approach (classical) §

“Traditional null hypothesis significance testing and related ideas. These ideas have been under attack for decades, most recently as being one cause of the scientific replicability problem.” - Some user on the orange site

Process §

• See good walkthrough of the process
• As a frequentist you don’t believe in anything before analyzing
• Always start with action instead of the hypothesis
• Step 1: Write down the default action
  • Default action is your cozy place. Incorrectly leaving it should be more painful than incorrectly sticking to it.
  • This is the action we choose
    • If we know nothing about the data
    • If we know partial things about the data (This is usually when we do inference)
    • If the result of the analysis falls in the bucket of null hypothesis (H0)
• Step 2: Write down the alternative action
  • This is the action we choose
    • If the result of the analysis falls in the bucket of alternative hypothesis (H1) i.e not in H0
• Step 3: Describe the null hypothesis(h0)
• Step 4: Describe the alternative hypothesis(h1)

Null Hypothesis §

• It is a set of possibilities
• Null hypothesis describes the full collection of universes in which you’d happily choose your default action.
• After the analysis, if h0 is accepted, we’ve learned nothing interesting. and that’s alright. We do the default action
• The hypothesis that there is no difference between things is called the Null Hypothesis.
  • The hypothesis: there is no difference
  • The test: We look for in the data if it convinces us to reject the hypothesis. i.e “Does the evidence that we collected make our null hypothesis look ridiculous?”. This is where p-value comes in.
• Null hypothesis (H0) is the mathematical compliment of the Alternative hypothesis (H1). i.e there’s no 3rd bucket
• Used to check if two things are different without using any preliminary data/test/experiment

p-value, significance level and confidence interval §

• When looking at the result of the analysis to check if the result can be accepted/rejected for the H0, we use p-value / confidence interval etc.
• Lower p-value => more further from H0
• confidence interval
  • the best guess is always in there
  • it’s narrower when there’s more data.

Mistakes / Errors §

These are again specific to frequentist stats

• Type I

  • Convicting an innocent person

• Type II

  • Failing to convict a guilty person

TODO Statistical Lies §

• People mistake p-values for p(hypothesis|data), mistake p-values for effect size (“it’s highly significant!”); moreover, people using NHST don’t understand multiplicity or “topping-off” problems.